関数 - ブログ1

三つのイメージ

イメージ1：機械

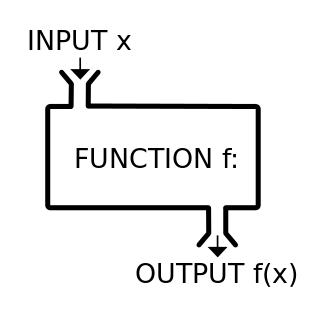
関数は機械や変換機と捉えることができる。ある機械に何かを放り込んで、その結果機械から何かが返ってくるというイメージ。この「機械に放り込む何か」は入力（input）と呼ばれ、「機械から返ってくる何か」が出力（output）と呼ばれる。（本ブログでは、関数のマシンチックな側面を強調するために、あえて「インプット」と「アウトプット」という表現をそれぞれ入力と出力の代わりに使うことがある。）

ここで重要なのは、関数が数学だけにしか存在しないと考えないことだ。広義に考えると、関数というのは、1) 入力があり、2) その入力値に対して何らかの処理をし、3) それを出力値として返す、機能のある全てを指す。よって、私たちが日常で使うものは大体関数だ。例えば、トースターがそうで、パンを焼くときトースターにパンと焼き加減を「入力」して、何らかの仕組みでそのパンがトーストされ、それが「出力」される。ここで重要なのは私たちは、パンがトーストされる仕組みを考えなくても（この仕組みを考えるのは工学と物理の分野だろう）、ただパンとボタン一つでパンを焼くことができるということだ。

リンゴを切る関数。（https://s3.us-west-2.amazonaws.com/参照）

このように、関数とは普通「使う」ものであって、その関数がどうやって入力値から出力値を計算したのかという実際の仕組みや実装（数式、アルゴリズム、モデルなど）を知る必要はない（知っていたらだめというわけではないが、知っていても知らなくても、使い方は変わらない）。言い換えれば、関数はブラックボックスなのだ。

イメージ2：写像

関数のもう少し厳格で数学的な見方が、写像（mapping）だ。（西村博之のように）写像という単語は聞いたこともないという人は多いと思う。イメージとしては、インプットとアウトプットを「結ぶ」ということだ。人によっては、英語のマッピングという単語の方がしっくりくるかもしれない。

一つ例を見てみる。

(wikipediaより)

このように写像はよく、二つの楕円とその中にある要素同士の矢印で可視化される。それぞれの入力に対応する、出力が矢印で結ばれている。この写像は「ある図形の色を返す関数」を表していることが分かるだろう。関数を写像で捉えると、後に説明する逆関数や合成関数などの可視化に役立つ。

写像についてもう少し踏み込んだ説明をしてみる。まず、全てのインプットの領域を定義域（domain）、すべてのアウトプットの領域を終域（codomain）と呼ぶ。例えば、上の例では、定義域は４つの図形、終域は５つの色だ。また、終域の中でも実際に対応する入力値があるものを値域 (image/range)と呼ぶ。ここで注意しないといけないのが、終域と値域の違いだ。終域とは、「この種類の、この範囲の値だったら、出力値として許される・想定される」と自分で指定するものだ。よって、実際の出力が終域外に存在することはありえない（プログラミングにおいては、指定した終域外の出力が存在する場合があって、それはエラーにあたる）。その一方で、値域とは、終域の要素の中でも、インプットから実際にマップされた要素の集まりを指す。つまり、出力値の集合だ。上の例では、赤と緑と黄には対応するインプット存在する一方、青と紫を持つ図形は存在しないため、値域は$\{赤, 緑, 黄\}$となる。

定義域、値域、終域の関係性を可視化すると次のようになる。入力値の集まりは定義域と等しい集合である一方、出力値の集まり（＝値域）は終域とは異なる集合である。具体的に言うと、値域は終域の部分集合だといえる。

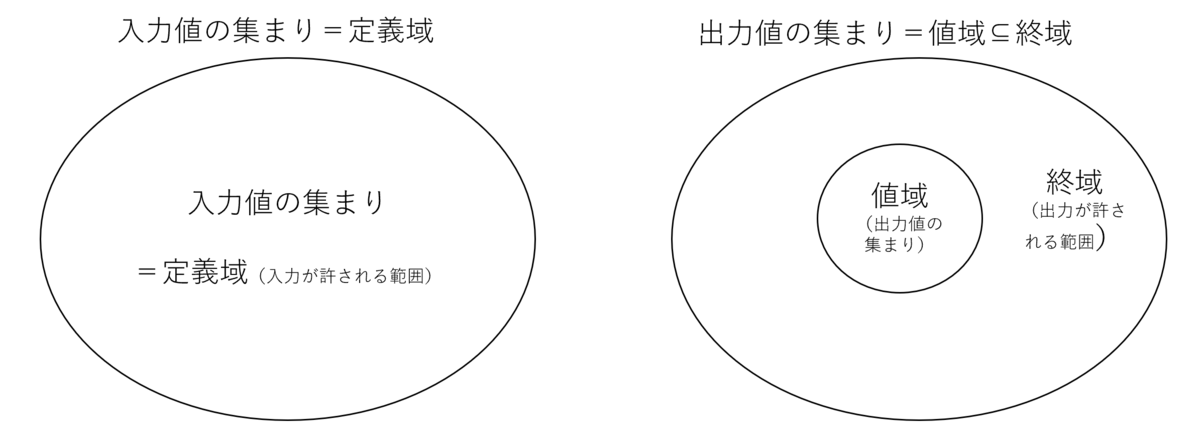
数学で一般的に見るような関数も同じように表してみる。例えば、定義域と終域のどちらも整数であった場合の、関数$f(x) = x^2$は以下のように可視化することができる。

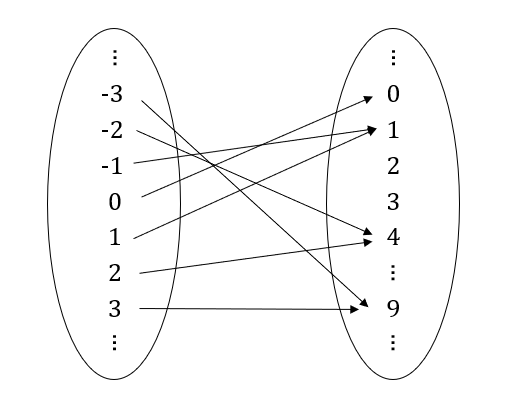
イメージ3：グラフ

高校の教科書で一番見られる可視化方法がグラフだ。以下は$f(x) = x^2$のプロットだ。

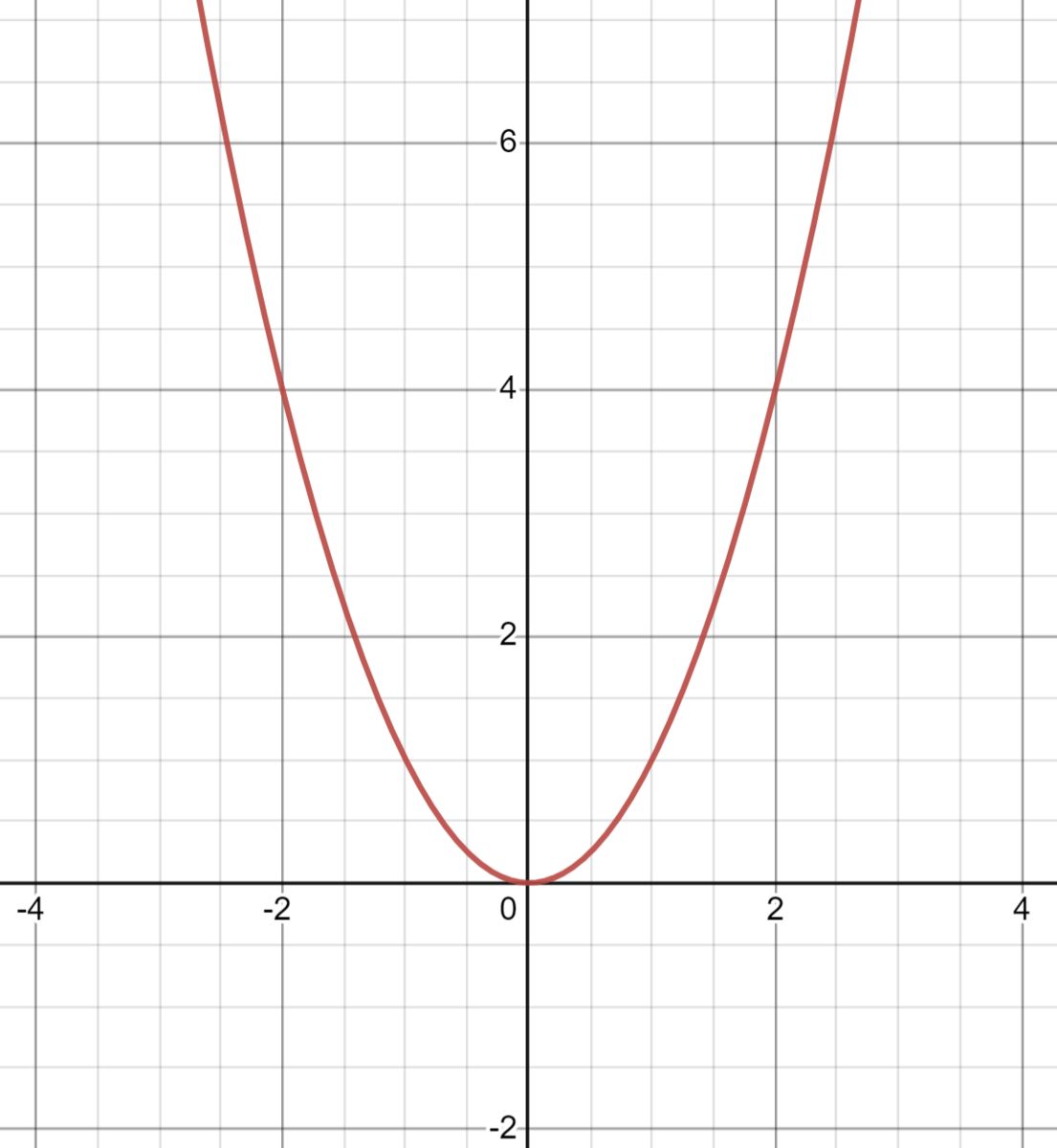
ここで、どうやってこのプロットができたのかを考えてみる。

$f(-3) = (-3)^2 = 9 → 点(-3, 9)$

$f(0) = 0^2 = 0 → 点(0, 0)$

$f(0.1) = 0.1^2 → 点(0.1, 0.01)$

$f(1) = 1^2 = 1 → 点(1, 1)$

$f(2) = 2^2 = 4 → 点(2, 4)$

このようにまず関数$f$にある値を入力し、出力を得る。そして、その（入力, 出力）のペアをグラフの点として扱っているというわけだ。これを定義域のすべての要素について行えば、私たちが想像する$f(x) = x^2$の綺麗な凹型の放物線が完成する。しかし、私たちが頭で想像するグラフを現実世界で完璧に再現するのは不可能な場合が多い。なぜならば多くの関数の定義域は$\mathbb{R}$や$\mathbb{Q}$であって、これらには無限のインプットが必用となるからだ。ここでいう無限には、二つの意味がある。一つは、+∞かつ-∞に発散するという意味だ（入力値を1000, 10000, 1000000, 1000000と永遠に増やすことができる）。二つ目に、ある二つの実数を選んだ時、その間に無限に数が存在する（例えば、1と2の間には、0.1, 0.2 .... 0.9とあり、さらに0.1と0.2の間には、0.01, 0.02...というように無限に数が存在する）。よって、コンピューターでグラフをプロットする際には、定義域の中でもスクリーンに映っている部分だけ（これは一つ目の問題を解決する）、1/100程度の間隔で関数に入力し（二つ目の問題を解決している）、それらをプロットしている。

三つのイメージを一つに

最初のイメージは、一つのインプットしか考えないためシンプルで「入力値を入れると出力値を返す」という概念的な側面が見えやすい。一方で、シンプルにした分、数学の厳密な定義を全て含んでいない。二つ目のイメージは、定義域と終域という概念も含めて関数を可視化している。機械の「入力値を入れると出力値を返す」というイメージよりも、ある値とある値が対応している、とか、結ばれている、というイメージを彷彿させる。最後のイメージは入力値が変化するにつれて、出力値がどう変化するかが分かりやすい。

関数を扱うときは、この三つのイメージを同時に思い出すと良いだろう。

数学的なな定義と表記

既に述べたが、関数は厳密には集合で定義される。関数は以下の三つから構成される1) 定義域を表す集合X、2)終域を表す集合Y、3)定義域の要素から終域の要素への対応を記す順序対（ordered pairs）。

①集合で表される、定義域： $\{x_1, x_2, x_3, ....\}$

②集合で表される、終域： $\{y_1, y_2, y_3, ....\}$

③順序対で表される、要素同士の対応：$\{(x_1, f(x_1)), (x_2, f(x_2)), (x_3, f(x_3)), ...\}$

高校数学では、関数は③のような表現の代わりに、$f(x) = x^2$のように要素同士の対応が数式で定義されることが多い。

先ほど挙げた値域は正確には③の順序対に含まれるf(x)の値の集まり（＝集合）のことを指す。また、関数fが定義域Xと終域Yから成り立つことを$f: X → Y$と表現する。例えば、定義域と終域の両方が実数なことを

$f: \mathbb{R} → \mathbb{R}$

と表現する。定義域と終域は、集合でさえあればなんでもよい。よって定義域と終域を以下のようにマニュアルで列挙することができる。

$f: \{1, 2, 3\} → \{4, 5, 6\}$

また、ある関数gに二つの入出力があり、それぞれ、整数と実数であった場合

$g: \mathbb{Z}×\mathbb{R}→ \mathbb{Z}×\mathbb{R}$

と表す。冒頭のトースターを関数と捉えたとき、定義域と終域は以下のように定義することができる。

$toaster: パン×\mathbb{Z}_{>0}→ パン$

高校数学などではこのような定義域と終域の明示的な指定がない場合がある。その場合、黙示的に、定義域はR、または出力が定義される（not undefined）一番大きい集合を指す。例えば、関数$f$が、$f(x) = x^2$と定義されていれば、定義域と終域は$\mathbb{R}$なことが分かる。一方で、関数$g$が、$g(x) = ln(x)$と定義されていた場合、黙示的に$g: {\{x∊\mathbb{R}⋀ x > 0\}→\mathbb{R}}$であることが分かる。

厳密には、関数は$f(x)$ではなく$f$で記載されるべきだ。f(x)というのは、任意のインプットxを代入したときに、帰ってくるアウトプットを一般的に表したものだ。一方で、$f$というのは、変換器自体のことを指すため、ある関数について触れる際は$f$とすべき。しかし、$f(x)$と$f$が区別なく使われることもよくある。このブログでは基本的には区別をつけない。

関数の条件

fが関数であるには二つの条件がある。一つは定義域内の要素全て（＝すべての入力値）に対応する要素（＝出力）が存在すること。

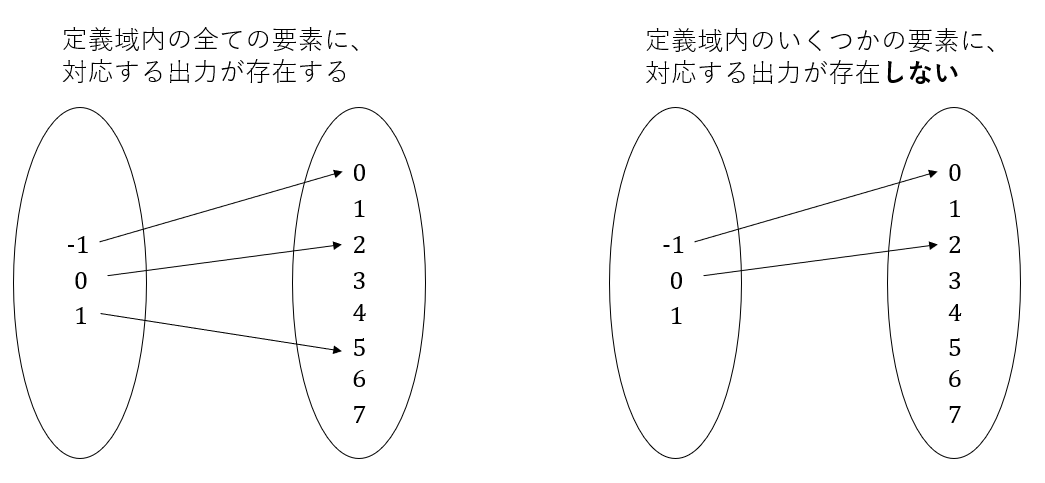
もし右の図の関数が存在したと仮定する。この機械に-1を入力すると、0が返ってくる。0を入力すると2が返ってくる。しかし、1を入力しても、対応する出力が存在しないため、何も返ってこない。このように、入力値を与えたのに、出力値が返ってこないというのは明らかに関数としては不備がある。

もう一つが、一つの入力に対して、一つだけの出力値しか存在しないことだ。

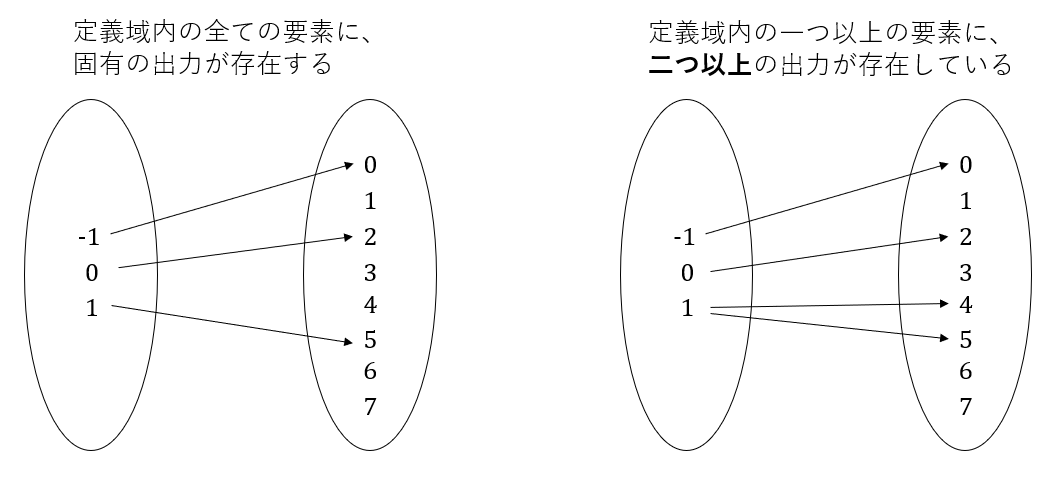
先ほどと同じように、右の関数が存在していたと仮定する。この機械に-1を入力すると、0が返ってくる。0を入力すると2が返ってくる。では、1を入力したときには何が返ってくるだろうか？図を見ると、1は4と5にマップされている。つまり、この関数に1を入力したとき、あるときは4が出力され、また違うときには5が出力されるということだ。これは一つの出力に答えが定まっていない（ambiguous）ということである。何度も言うように、関数というのは機械だ。同じ入力値を与えたのに、違う出力値が出てきてしまっては使う側としては困る（トースターに同じパンを入れ５分と設定したら、毎回同じ焼き加減であることを期待するだろう。逆にそうでなかったら、普通誤作動・故障していると考える。）。

この条件はグラフでも理解することができる。

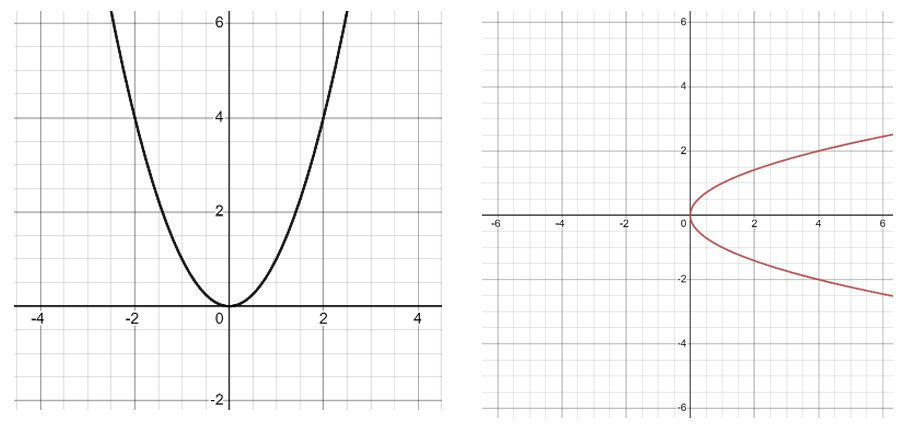
左のグラフは、それぞれのxについて一つの出力値しかないため、関数であるといえる。一方で、右のグラフは（0を除く）それぞれのxについて対応する二つの出力値があることが分かる。例えば、$x = 4$に対応するy値は2と-2だ。よってこのグラフは関数を表すものではない。実は右のグラフは$y =\sqrt{x}$のグラフである（注意したいのは、ここであえて$f(x) =\sqrt{x}$と表現するのではなく、$y =\sqrt{x}$と表現していることだ。xとyの関係性を結ぶだけであれば（＝図形に注目したい場合）、関数の条件を気にする必要はない。）。 $y=\sqrt{x}$という方程式を解いたとき（$x = 0$でない限り）答えは＋と－の二つになる。だから一つのx値について二つのy値が存在しているのだ。

グラフを使い図形の関数判断をする方法を一般化させたものに、"Vertical Line Test"がある。「同じ入力に対して、二つ以上の出力が無い」というのを言い換えれば、y軸と垂直な直線を用意してグラフの上を左右したとき、その直線の上に二つ以上の点が存在しないということ。よって、グラフのy軸と平行に指を左右に動かし、もし重なった部分があれば、その図形関数でないということが分かる。

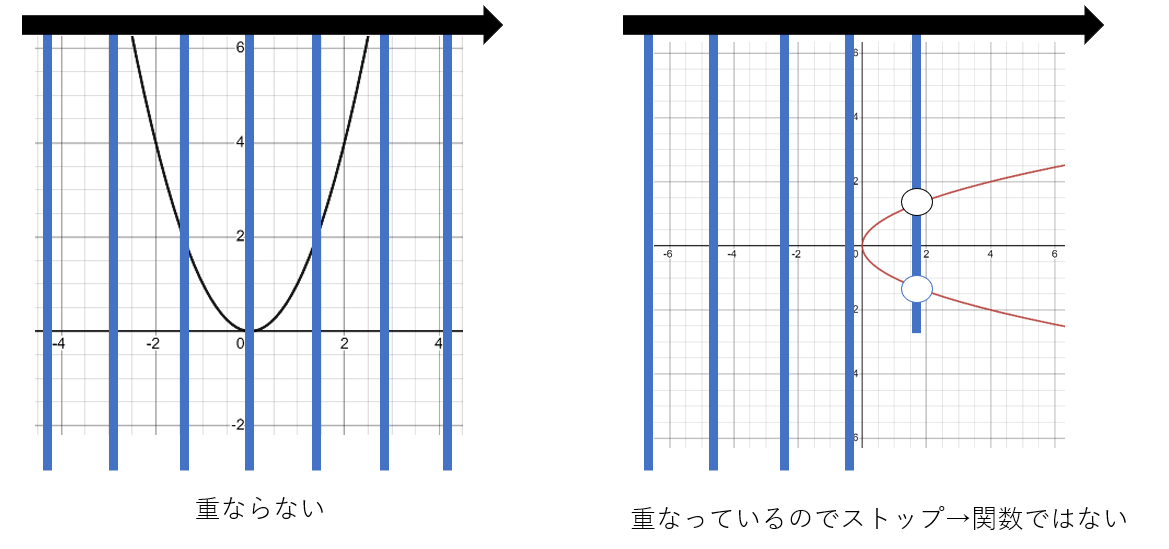
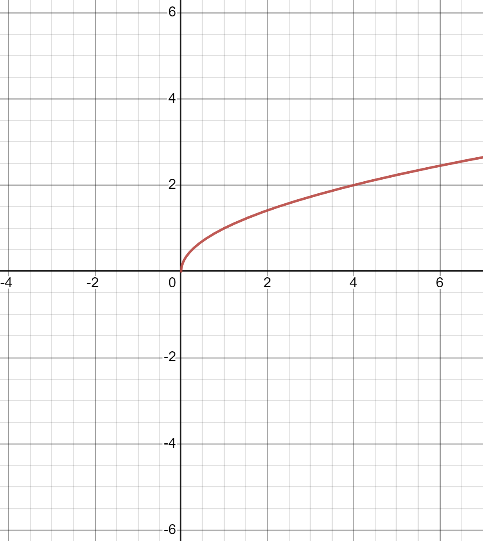
右のグラフのように、グラフ上で図形として存在し、一見関数のように見えるが、実はそうではないものは無数にある。このような図形を関数に直すには、定義域や終域またはマッピング自体を変える必要がある。例えば、右のグラフの場合を考える。この図形は順序対で表現すると、$\{(0, 0), ..., (1, (1, -1)), ...(2, (2, -2)), ...)\}$のように、(0を除いた)それぞれの入力について二つの出力値があり、これを一つにすればいい。これにはマッピングの変更が必用で、例えば、$f(x) = |\sqrt{x}|$や、$f(x) = \{y| y = \sqrt{x} ⋀ y>=0\})$ （これは二つの答えの中でも０以上の数字だけ返すという意味）（両方とも定義域は0以上）とすることでこの問題が解決する。これをグラフにすると、元の図形の上半分だけ残った形ができる。

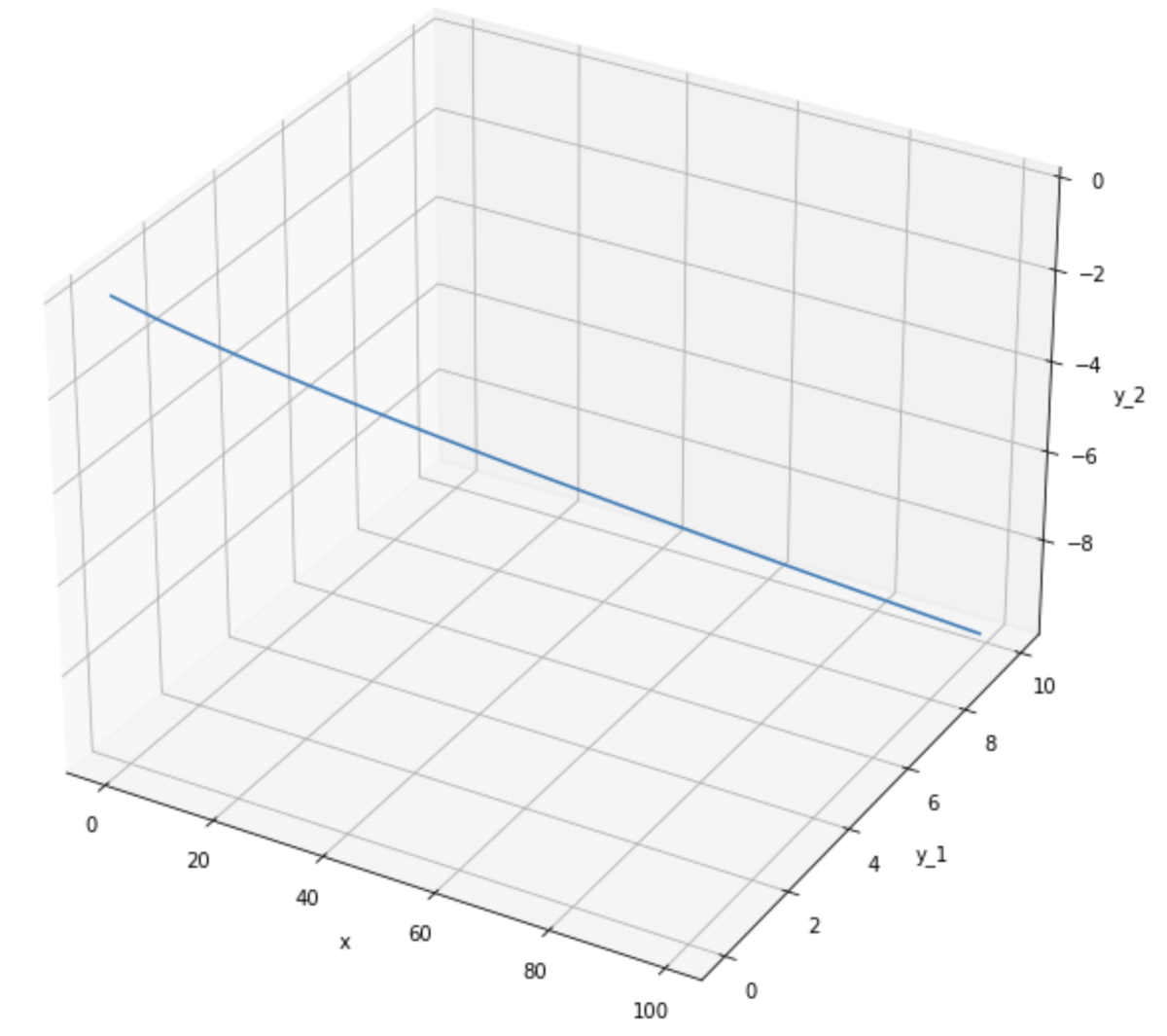
また、終域を順序対$(y_1, y_2)$と設定することでも、$y = \sqrt{x}$を関数にすることができる。これは形式的に$f: \{x\ |\ x \geq 0 \land x \in \mathbb{R}\} → (\mathbb{R}, \mathbb{R})$と表現され、この関数に0から100まで入力すると以下のようなプロットができる。

もし数学書などで$f(x) = \sqrt{x}$との記載があった場合（上で述べてるように実際の$y=\sqrt{x}$は関数ではない）、黙示的に$f(x) =| \sqrt{x}|$を意味する場合が多く、グラフも先ほどのものになる。これはよく使う$\sqrt{x}$を関数としてできるだけ簡潔に表現するためだと思われる。

まとめると、関数fが満たす必要のある条件は二つある。一つ目に、 f(x)は出力値を返さないといけない。例えば、順序対$\{(0, ), ..., (1, ), ...(2, 2), ...)\}$は関数ではない。二つ目に、f(x)は一つの出力値だけを返さないといけない。例えば順序対$\{(0, 0), ..., (1, (1, -1)), ...(2, (2, -2)), ...)\}$は関数ではない。※注意：二つ目の条件は一つ目の条件を包括するため、関数が満たす条件が「f(x)は一つの出力値だけを返さないといけない」とだけ記載のある教科書もある。