JavaScript Promiseについて

asynchronousをやるときに必用なのがpromise。

1. Promiseはあとで実行する関数を保存するオブジェクト。
2. Promise自体は関数を保存するオブジェクトなだけだから、それを作っただけでは関数は起動しない。
3. .then()または.catch()をその作ったpromiseオブジェクトに使うことで、初めてそのpromiseオブジェクトに保存されてる関数が実行される。
4. Promiseを定義するときに、その中には、必ずresolve・reject関数が必用。これらは、そのpromiseがいつ終わるのかを指定する。（実際にはそのpromiseのstateをpendingからfulfilledまたはrejectedに変える。javascriptはpeomiseのstateがfulfilledか、rejectedに変わったら、自動的にそのpromiseを終了させる）

一般的なpromiseの作り方。
const myPromise = new Promise*1;
});

一般的なpromiseの起動のしかた。
promise.then(value => console.log(value))

ちなみに：
fetch()自体は関数だけど、fetchがreturnするのはpromise。だから、fetch("https/somethig")はまだHTTP requestをしない。fetch("https/something").then()を使うことで初めて、network requestをする。

fetchのsample implementationはこんな感じ。

function fetch(url) {
  return new Promise*2;
      }
    };
    xhr.onerror = () => reject(new Error("Network Error"));
    xhr.send();
  });
}

*1:resolve, reject) => {
  // Do some asynchronous work...

  // If the work is successful, call the resolve function with a value
  resolve('Success!');

  // If the work fails, call the reject function with an error
  // reject(new Error('Something went wrong!'

*2:resolve, reject) => {
    const xhr = new XMLHttpRequest();
    xhr.open("GET", url);
    xhr.onload = () => {
      if (xhr.status >= 200 && xhr.status < 300) {
        resolve(xhr.response);
      } else {
        reject(new Error(xhr.statusText

関数

三つのイメージ

イメージ1：機械

(wikipedia参照)

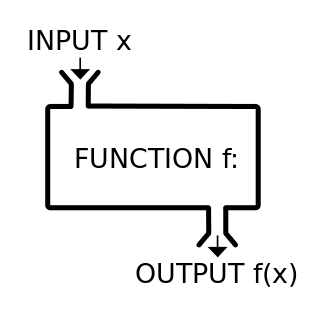
関数は機械や変換機と捉えることができる。ある機械に何かを放り込んで、その結果機械から何かが返ってくるというイメージ。この「機械に放り込む何か」は入力（input）と呼ばれ、「機械から返ってくる何か」が出力（output）と呼ばれる。（本ブログでは、関数のマシンチックな側面を強調するために、あえて「インプット」と「アウトプット」という表現をそれぞれ入力と出力の代わりに使うことがある。）

ここで重要なのは、関数が数学だけにしか存在しないと考えないことだ。広義に考えると、関数というのは、1) 入力があり、2) その入力値に対して何らかの処理をし、3) それを出力値として返す、機能のある全てを指す。よって、私たちが日常で使うものは大体関数だ。例えば、トースターがそうで、パンを焼くときトースターにパンと焼き加減を「入力」して、何らかの仕組みでそのパンがトーストされ、それが「出力」される。ここで重要なのは私たちは、パンがトーストされる仕組みを考えなくても（この仕組みを考えるのは工学と物理の分野だろう）、ただパンとボタン一つでパンを焼くことができるということだ。

リンゴを切る関数。（https://s3.us-west-2.amazonaws.com/参照）

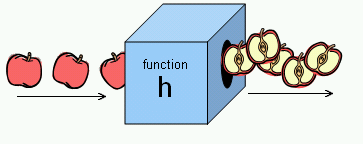
このように、関数とは普通「使う」ものであって、その関数がどうやって入力値から出力値を計算したのかという実際の仕組みや実装（数式、アルゴリズム、モデルなど）を知る必要はない（知っていたらだめというわけではないが、知っていても知らなくても、使い方は変わらない）。言い換えれば、関数はブラックボックスなのだ。

イメージ2：写像

関数のもう少し厳格で数学的な見方が、写像（mapping）だ。（西村博之のように）写像という単語は聞いたこともないという人は多いと思う。イメージとしては、インプットとアウトプットを「結ぶ」ということだ。人によっては、英語のマッピングという単語の方がしっくりくるかもしれない。

一つ例を見てみる。

(wikipediaより)

このように写像はよく、二つの楕円とその中にある要素同士の矢印で可視化される。それぞれの入力に対応する、出力が矢印で結ばれている。この写像は「ある図形の色を返す関数」を表していることが分かるだろう。関数を写像で捉えると、後に説明する逆関数や合成関数などの可視化に役立つ。

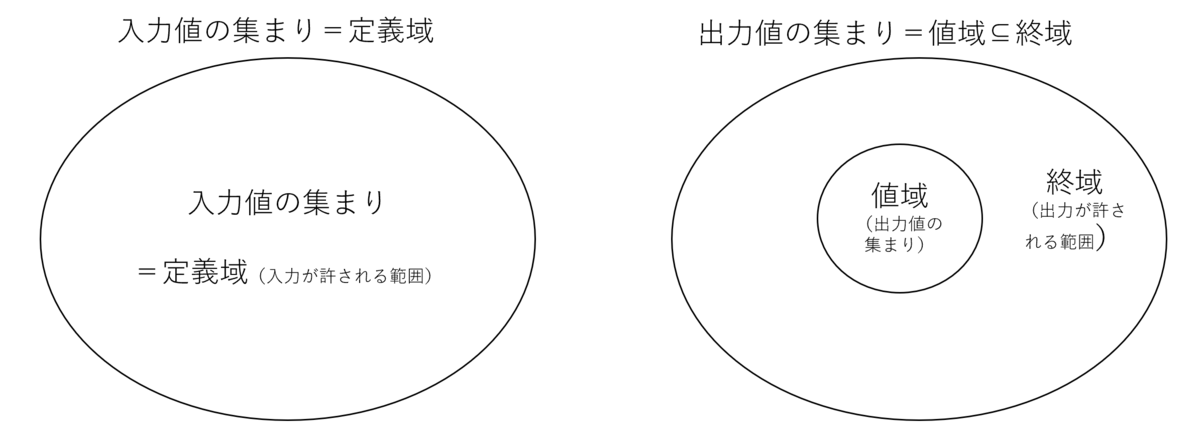
写像についてもう少し踏み込んだ説明をしてみる。まず、全てのインプットの領域を定義域（domain）、すべてのアウトプットの領域を終域（codomain）と呼ぶ。例えば、上の例では、定義域は４つの図形、終域は５つの色だ。また、終域の中でも実際に対応する入力値があるものを値域 (image/range)と呼ぶ。ここで注意しないといけないのが、終域と値域の違いだ。終域とは、「この種類の、この範囲の値だったら、出力値として許される・想定される」と自分で指定するものだ。よって、実際の出力が終域外に存在することはありえない（プログラミングにおいては、指定した終域外の出力が存在する場合があって、それはエラーにあたる）。その一方で、値域とは、終域の要素の中でも、インプットから実際にマップされた要素の集まりを指す。つまり、出力値の集合だ。上の例では、赤と緑と黄には対応するインプット存在する一方、青と紫を持つ図形は存在しないため、値域は$\{赤, 緑, 黄\}$となる。

定義域、値域、終域の関係性を可視化すると次のようになる。入力値の集まりは定義域と等しい集合である一方、出力値の集まり（＝値域）は終域とは異なる集合である。具体的に言うと、値域は終域の部分集合だといえる。

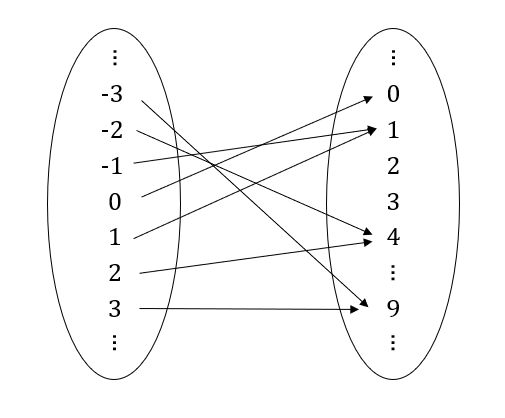
数学で一般的に見るような関数も同じように表してみる。例えば、定義域と終域のどちらも整数であった場合の、関数$f(x) = x^2$は以下のように可視化することができる。

イメージ3：グラフ

高校の教科書で一番見られる可視化方法がグラフだ。以下は$f(x) = x^2$のプロットだ。

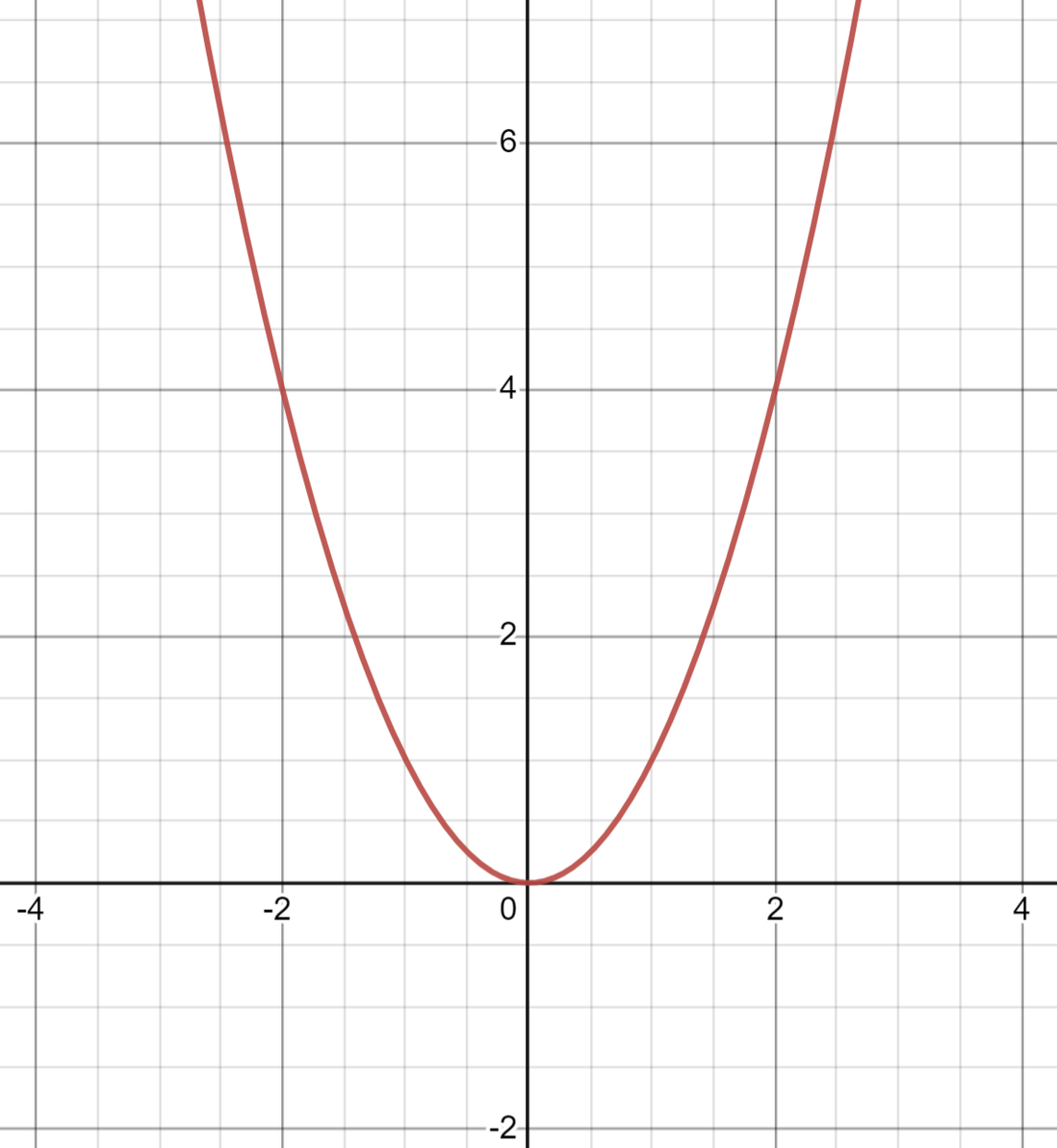
ここで、どうやってこのプロットができたのかを考えてみる。

$f(-3) = (-3)^2 = 9 → 点(-3, 9)$

$f(0) = 0^2 = 0 → 点(0, 0)$

$f(0.1) = 0.1^2 → 点(0.1, 0.01)$

$f(1) = 1^2 = 1 → 点(1, 1)$

$f(2) = 2^2 = 4 → 点(2, 4)$

このようにまず関数$f$にある値を入力し、出力を得る。そして、その（入力, 出力）のペアをグラフの点として扱っているというわけだ。これを定義域のすべての要素について行えば、私たちが想像する$f(x) = x^2$の綺麗な凹型の放物線が完成する。しかし、私たちが頭で想像するグラフを現実世界で完璧に再現するのは不可能な場合が多い。なぜならば多くの関数の定義域は$\mathbb{R}$や$\mathbb{Q}$であって、これらには無限のインプットが必用となるからだ。ここでいう無限には、二つの意味がある。一つは、+∞かつ-∞に発散するという意味だ（入力値を1000, 10000, 1000000, 1000000と永遠に増やすことができる）。二つ目に、ある二つの実数を選んだ時、その間に無限に数が存在する（例えば、1と2の間には、0.1, 0.2 .... 0.9とあり、さらに0.1と0.2の間には、0.01, 0.02...というように無限に数が存在する）。よって、コンピューターでグラフをプロットする際には、定義域の中でもスクリーンに映っている部分だけ（これは一つ目の問題を解決する）、1/100程度の間隔で関数に入力し（二つ目の問題を解決している）、それらをプロットしている。

三つのイメージを一つに

最初のイメージは、一つのインプットしか考えないためシンプルで「入力値を入れると出力値を返す」という概念的な側面が見えやすい。一方で、シンプルにした分、数学の厳密な定義を全て含んでいない。二つ目のイメージは、定義域と終域という概念も含めて関数を可視化している。機械の「入力値を入れると出力値を返す」というイメージよりも、ある値とある値が対応している、とか、結ばれている、というイメージを彷彿させる。最後のイメージは入力値が変化するにつれて、出力値がどう変化するかが分かりやすい。

関数を扱うときは、この三つのイメージを同時に思い出すと良いだろう。

数学的なな定義と表記

既に述べたが、関数は厳密には集合で定義される。関数は以下の三つから構成される1) 定義域を表す集合X、2)終域を表す集合Y、3)定義域の要素から終域の要素への対応を記す順序対（ordered pairs）。

①集合で表される、定義域： $\{x_1, x_2, x_3, ....\}$

②集合で表される、終域： $\{y_1, y_2, y_3, ....\}$

③順序対で表される、要素同士の対応：$\{(x_1, f(x_1)), (x_2, f(x_2)), (x_3, f(x_3)), ...\}$

高校数学では、関数は③のような表現の代わりに、$f(x) = x^2$のように要素同士の対応が数式で定義されることが多い。

先ほど挙げた値域は正確には③の順序対に含まれるf(x)の値の集まり（＝集合）のことを指す。また、関数fが定義域Xと終域Yから成り立つことを$f: X → Y$と表現する。例えば、定義域と終域の両方が実数なことを

$f: \mathbb{R} → \mathbb{R}$

と表現する。定義域と終域は、集合でさえあればなんでもよい。よって定義域と終域を以下のようにマニュアルで列挙することができる。

$f: \{1, 2, 3\} → \{4, 5, 6\}$

また、ある関数gに二つの入出力があり、それぞれ、整数と実数であった場合

$g: \mathbb{Z}×\mathbb{R}→ \mathbb{Z}×\mathbb{R}$

と表す。冒頭のトースターを関数と捉えたとき、定義域と終域は以下のように定義することができる。

$toaster: パン×\mathbb{Z}_{>0}→ パン$

高校数学などではこのような定義域と終域の明示的な指定がない場合がある。その場合、黙示的に、定義域はR、または出力が定義される（not undefined）一番大きい集合を指す。例えば、関数$f$が、$f(x) = x^2$と定義されていれば、定義域と終域は$\mathbb{R}$なことが分かる。一方で、関数$g$が、$g(x) = ln(x)$と定義されていた場合、黙示的に$g: {\{x∊\mathbb{R}⋀ x > 0\}→\mathbb{R}}$であることが分かる。

厳密には、関数は$f(x)$ではなく$f$で記載されるべきだ。f(x)というのは、任意のインプットxを代入したときに、帰ってくるアウトプットを一般的に表したものだ。一方で、$f$というのは、変換器自体のことを指すため、ある関数について触れる際は$f$とすべき。しかし、$f(x)$と$f$が区別なく使われることもよくある。このブログでは基本的には区別をつけない。

関数の条件

fが関数であるには二つの条件がある。一つは定義域内の要素全て（＝すべての入力値）に対応する要素（＝出力）が存在すること。

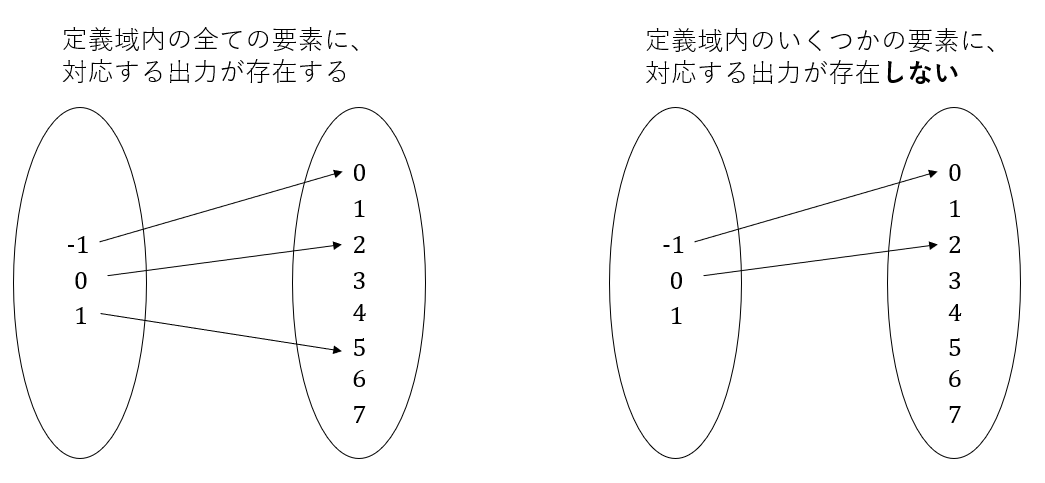
もし右の図の関数が存在したと仮定する。この機械に-1を入力すると、0が返ってくる。0を入力すると2が返ってくる。しかし、1を入力しても、対応する出力が存在しないため、何も返ってこない。このように、入力値を与えたのに、出力値が返ってこないというのは明らかに関数としては不備がある。

もう一つが、一つの入力に対して、一つだけの出力値しか存在しないことだ。

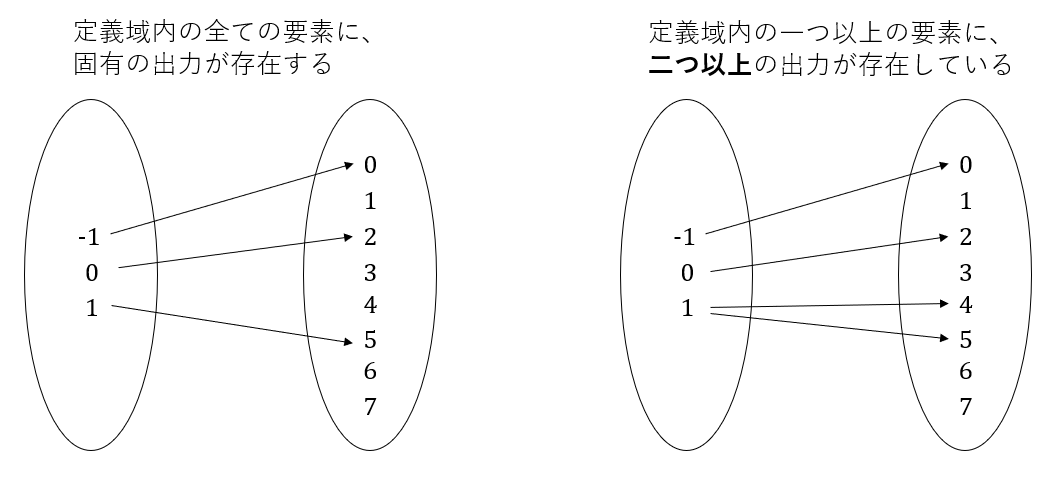
先ほどと同じように、右の関数が存在していたと仮定する。この機械に-1を入力すると、0が返ってくる。0を入力すると2が返ってくる。では、1を入力したときには何が返ってくるだろうか？図を見ると、1は4と5にマップされている。つまり、この関数に1を入力したとき、あるときは4が出力され、また違うときには5が出力されるということだ。これは一つの出力に答えが定まっていない（ambiguous）ということである。何度も言うように、関数というのは機械だ。同じ入力値を与えたのに、違う出力値が出てきてしまっては使う側としては困る（トースターに同じパンを入れ５分と設定したら、毎回同じ焼き加減であることを期待するだろう。逆にそうでなかったら、普通誤作動・故障していると考える。）。

この条件はグラフでも理解することができる。

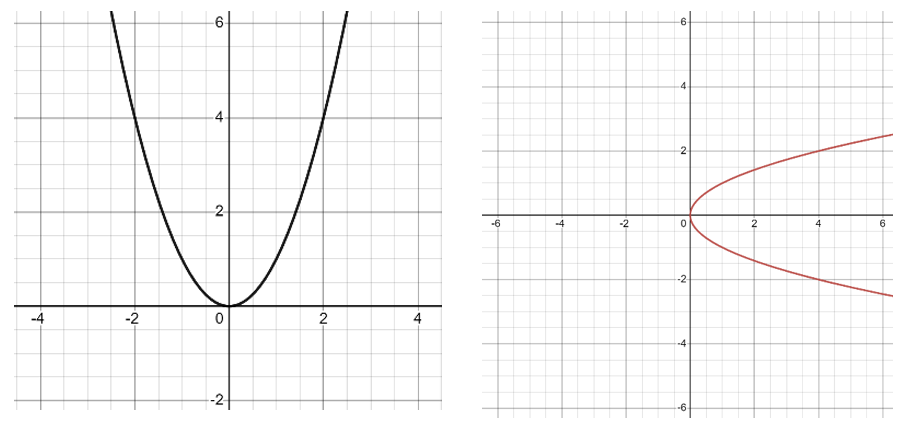
左のグラフは、それぞれのxについて一つの出力値しかないため、関数であるといえる。一方で、右のグラフは（0を除く）それぞれのxについて対応する二つの出力値があることが分かる。例えば、$x = 4$に対応するy値は2と-2だ。よってこのグラフは関数を表すものではない。実は右のグラフは$y =\sqrt{x}$のグラフである（注意したいのは、ここであえて$f(x) =\sqrt{x}$と表現するのではなく、$y =\sqrt{x}$と表現していることだ。xとyの関係性を結ぶだけであれば（＝図形に注目したい場合）、関数の条件を気にする必要はない。）。 $y=\sqrt{x}$という方程式を解いたとき（$x = 0$でない限り）答えは＋と－の二つになる。だから一つのx値について二つのy値が存在しているのだ。

グラフを使い図形の関数判断をする方法を一般化させたものに、"Vertical Line Test"がある。「同じ入力に対して、二つ以上の出力が無い」というのを言い換えれば、y軸と垂直な直線を用意してグラフの上を左右したとき、その直線の上に二つ以上の点が存在しないということ。よって、グラフのy軸と平行に指を左右に動かし、もし重なった部分があれば、その図形関数でないということが分かる。

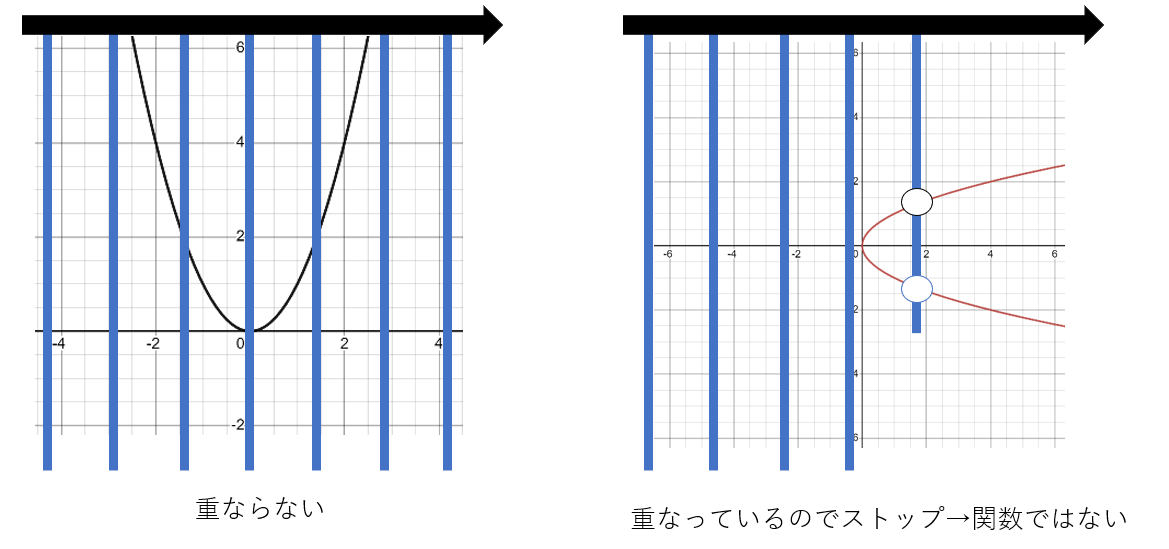
右のグラフのように、グラフ上で図形として存在し、一見関数のように見えるが、実はそうではないものは無数にある。このような図形を関数に直すには、定義域や終域またはマッピング自体を変える必要がある。例えば、右のグラフの場合を考える。この図形は順序対で表現すると、$\{(0, 0), ..., (1, (1, -1)), ...(2, (2, -2)), ...)\}$のように、(0を除いた)それぞれの入力について二つの出力値があり、これを一つにすればいい。これにはマッピングの変更が必用で、例えば、$f(x) = |\sqrt{x}|$や、$f(x) = \{y| y = \sqrt{x} ⋀ y>=0\})$ （これは二つの答えの中でも０以上の数字だけ返すという意味）（両方とも定義域は0以上）とすることでこの問題が解決する。これをグラフにすると、元の図形の上半分だけ残った形ができる。

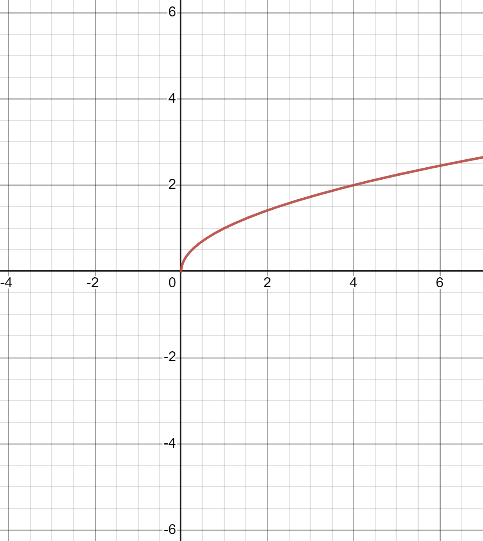
また、終域を順序対$(y_1, y_2)$と設定することでも、$y = \sqrt{x}$を関数にすることができる。これは形式的に$f: \{x\ |\ x \geq 0 \land x \in \mathbb{R}\} → (\mathbb{R}, \mathbb{R})$と表現され、この関数に0から100まで入力すると以下のようなプロットができる。

もし数学書などで$f(x) = \sqrt{x}$との記載があった場合（上で述べてるように実際の$y=\sqrt{x}$は関数ではない）、黙示的に$f(x) =| \sqrt{x}|$を意味する場合が多く、グラフも先ほどのものになる。これはよく使う$\sqrt{x}$を関数としてできるだけ簡潔に表現するためだと思われる。

まとめると、関数fが満たす必要のある条件は二つある。一つ目に、 f(x)は出力値を返さないといけない。例えば、順序対$\{(0, ), ..., (1, ), ...(2, 2), ...)\}$は関数ではない。二つ目に、f(x)は一つの出力値だけを返さないといけない。例えば順序対$\{(0, 0), ..., (1, (1, -1)), ...(2, (2, -2)), ...)\}$は関数ではない。※注意：二つ目の条件は一つ目の条件を包括するため、関数が満たす条件が「f(x)は一つの出力値だけを返さないといけない」とだけ記載のある教科書もある。

関数をもっと理解するために

関数のイメージを多少持った時に、自然に出てくる疑問はいくつかある。

1) 一つの関数の結果をもう一つの関数の入力として扱いたい。（トースターに入れ、焼かれたパンを細切れにしたかったとする。）

2) 入力→出力の逆をたどることはできるか（ある別の機械に焼かれたパンを入れると、焼かれる前のパンと、何分焼いたのかという数字を出力する）

3) インプットをちょっとだけ変えたときに（これは特に定義域と終域が$\mathbb{R}$だった場合）、それに比較して、アウトプットはどれくらい変わるだろうか（焼く時間をちょっと変えると、どれくらいパンの焼き目が変わるか）。

4) インプットを増やすと、同じ分だけアウトプットが増える関数。インプットを増やせば増やすほど、急激にアウトプットが増える関数。周期性（一定のリズム）でアウトプットが変化する関数。など、代表的な関数がいくつかありそう。

5) インプットが二つ以上ある場合はどうなるのだろう。（もともとトースターの例には二つの入力値がったーパンとトースト時間）

運のいいことに、これらの疑問に対して先人たちが既に答えを用意してくれている。僕もこれらについて説明してみた。

1) 合成関数: 一つの関数のアウトプットをもう一つの関数のインプットと捉える
2) 逆関数：アウトプットからインプットの写像、逆写像

3) 微分：インプットをちょっと変えるとアウトプットがどう変わるか

4) 初等関数：代表的な関数の種類、特にe^x、logx, sinx, cosx。

5) 多変数関数（multivariable functions）

合成関数と連鎖法則

単射・全射性と逆関数

微分

三角関数

-----

Python: オブジェクトのコピー

疑問

Intとlistではコピーしたときの挙動が違うように見える。

というのも、リストをコピーしたと思ったら元の変数が指すリストも変わってることがあることを経験したことがあるだろう。

これはなぜか？

答え

前提1: pythonの変数はポインターであって、変数自体がオブジェクトを持っているわけではない。

前提2: pythonでは、同じ数字を表すintオブジェクトは一つしか存在しない。一方で、listオブジェクトの場合、同じ要素で構成されるリストはいくつでも存在可能。

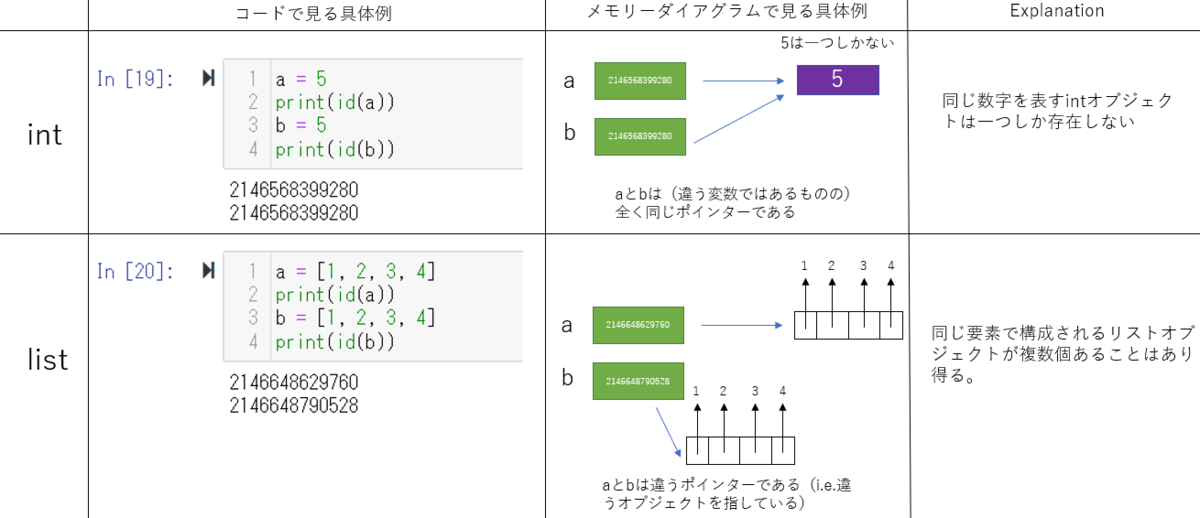
intの場合

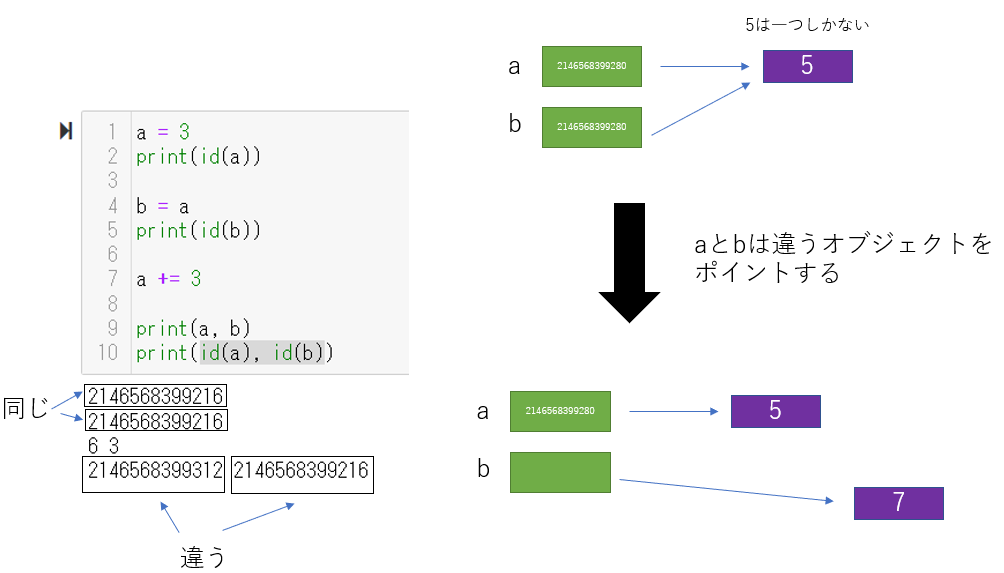
同じ数字を表すintオブジェクトは一つしか存在しない。もし違う二つの変数(例えば変数aとb)の両方に同じ数値をassignした場合、両方とも同じオブジェクトをポイントしている。ここで、片方の変数(ここでは変数aとする)を違う値をassignしたり、incrementしたとする。このときpythonは：

1) 新しい数値のオブジェクトを作る。

2) 変数aは1)で作ったオブジェクトをポイントする。

つまり変数bのポインターは変わっていないし、ポイントしている先のオブジェクトにも変化はないということ。変わったのは変数aだけ。

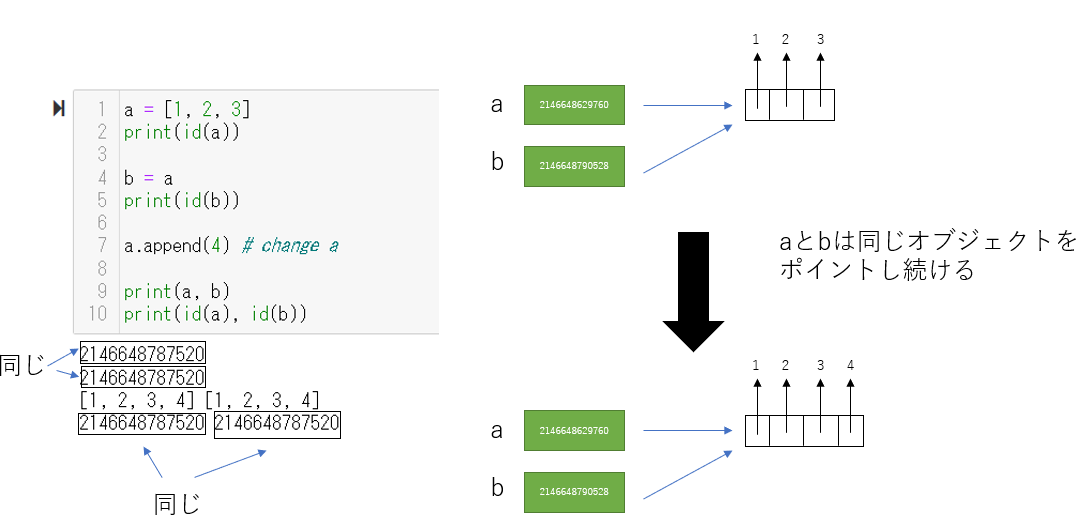
listの場合

同じリスト（＝同じ要素から成り立つリストオブジェクト）は何個でも存在することができる。intオブジェクトの場合と同じように二つの変数があり、両方とも、同じlistオブジェクトをポイントしていたとする。このとき、片方の変数の要素の一部（または全て）を変えたとする。このとき変数aもbも同じオブジェクトを指しているのだから、print(b)をすると、aと同じオブジェクトが出力される。

結論

結局なんでこのような現象が起きるのか？

どちらかというと特殊なのはintだといえる。「a += 3」としたとき、変数aがポイントするオブジェクトの値を変えるのではなく、新しいオブジェクトを作って（もしもともとaが5だとすれば、8というintオブジェクトをつくる）、それをポイントする。一方でリストは、要素を変えるときに、わざわざ新しいオブジェクトを作るのではなく、単純に、ポイントしているオブジェクトの要素を変える。

「飢えている人がいるときに、魚を与えるか、魚の釣り方を教えるか。」

「飢えている人がいるときに、魚を与えるか、魚の釣り方を教えるか。」

「飢えている人がいるときに、魚を与えるか、魚の釣り方を教えるか。」という話で、老子は「人に魚を与えれば一日で食べてしまうが、釣り方を教えれば一生食べていける」と言うわけだがこの考え方は現代社会では通用しない。昔と違い技術革新を繰り返してきた現在の社会では、金になる知識を理解するにはいくらかの頭の良さが必要だ。頭の悪い人にいくら複雑なことを教えても分からない。

世の中には生まれてきた環境が悪いせいで本領が発揮できていない人材もいる。ホームレスや社畜が全員本質的に頭が悪いとは限らない。親とか学校とか友達とかそういう環境に恵まれなかったから、本領が発揮できていないのかもしれない。だがら前提として、教育費の補償は大事だ。

しかし、いくら最高の教育を全員に施したところで、究極的に頭の悪い人はどうしようもないのだ。であれば、その一部分の人間には定期的に魚を恵んであげればよいだけだ。

この見方は「すばらしい新世界」でも見られる階級思想だ。アルファ階級は知的であり、社会のリーダーであり幸せだ。その一方でエプシロン階級は少しの単純労働と後は遊び惚けることができる。つまり頭が悪い人も良いとも皆が幸せな世界なのだ。

わざわざ明確な階級をつくる必要はないが（もちろんわれわれ人間は物語のような人工物ではないため、階層同士の対立が起こりうる可能性がある）、社会を引っ張っていく人と、それについていく人という大まかな二つの人種がいてもよいのではないか。頭がよい人はただでさえ特をしているのだから、彼らは頭の悪い人を引っ張っていくことくらいしてもよいはずだ。

この考え方を現実世界に落とし込むと、セーフティネットやベーシックインカム＋「ニート＝悪」という価値観の払拭となるのではないか。

ユークリッドの互換法

この投稿では、ユークリッドの互除法を説明する。

ユークリッドの互除法は二つの正整数の最大公約数を求めるアルゴリズムだ。よって、冒頭で正整数を説明し、さらに最大公約数について説明した後、アルゴリズム自体について説明しようと思う。

整数

整数は分数無しでも表せる数のことを指す。さらに重要なのが、整数は以下のようにある約数qの倍数であるということ。「$q$は$b$の約数」であると同時に、「$b$は$q$の倍数」でもある。（$a$,、$b$、$q$はすべて整数）

$$ b=qa $$

この表現を可視化すると、以下のようになる。

つまり、整数というのは本質的に、ある約数という名のブロックの積み重ねなのだ。

そして、当たり前ではあるが、このブロックの種類は、それぞれの整数によっていくつか考えることができる。例えば12は以下のように6通りのブロックが考えられるだろう。

\begin{align} 12 = \begin{cases} 1×12 \cr 2×6 \cr 3×4 \cr 4×3 \cr 6×2 \cr 12×1 \end{cases} \end{align}

これを先ほどのようにブロックで表すと、同じ整数を違うブロックの積み重なりで表すことができることが分かる。

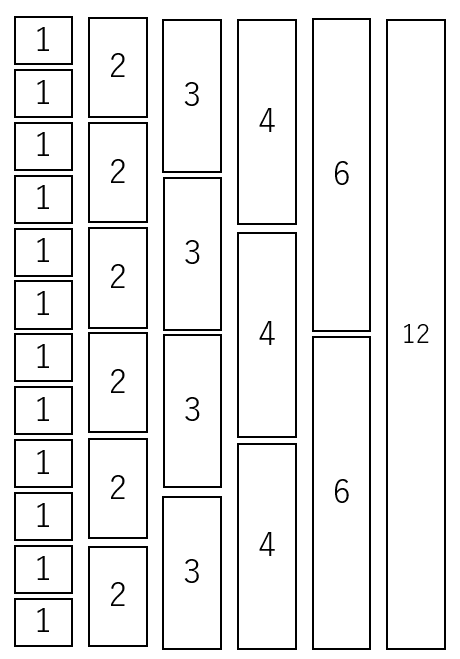
整数の本質がブロックの積み重なりだということを理解すると、ユークリッドの互除法は理解しやすくなる。

最大公約数(gcd)

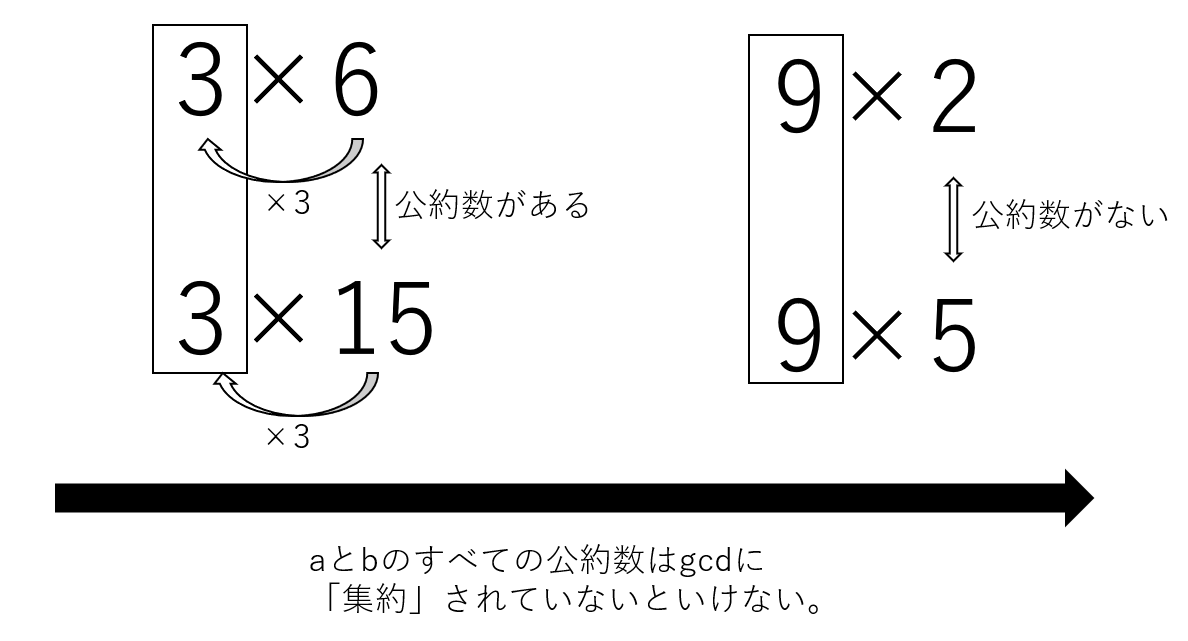
最大公約数は「二つの整数が持つ共通の公約数の中でも最大のもの」を指す。上で述べたように、整数は「ある約数$q$の倍数」という形で表すことができる。よって、ある正整数$a$と$b$を二つの最大公約数の倍数($g$)であることは以下のように表現できる。

\begin{align} \begin{cases} a=g×m \cr b=g×n \end{cases} \end{align}

この時、$ m $と$n$は定数であり、必ず互いに素(coprime)になる。これは、gcdは二つの整数の「最大」約数でなければいけないからだ。言い換えれば、aとbのすべての公約数は最大公約数gに「集約」されていないといけないのだ。

整数はさまざまな約数qの倍数であって、qは必ずしも1つと決定しているわけではない。何らかのプロセスを経て、最適なq、すなわち最大公約数gを見つける必要がある。正整数aとbはそれぞれ違うqで表現できる。その中でも共通かつ最大のqを見つけるというわけだ。これは、最大のブロックを見つけるの同義だ。例えば、a = 12とb=8はそれぞれ、{1, 2, 3, 4, 6 ,12}と{1, 2, 4, 8}と約数qが複数個存在するが、この場合最適なqは4だ。

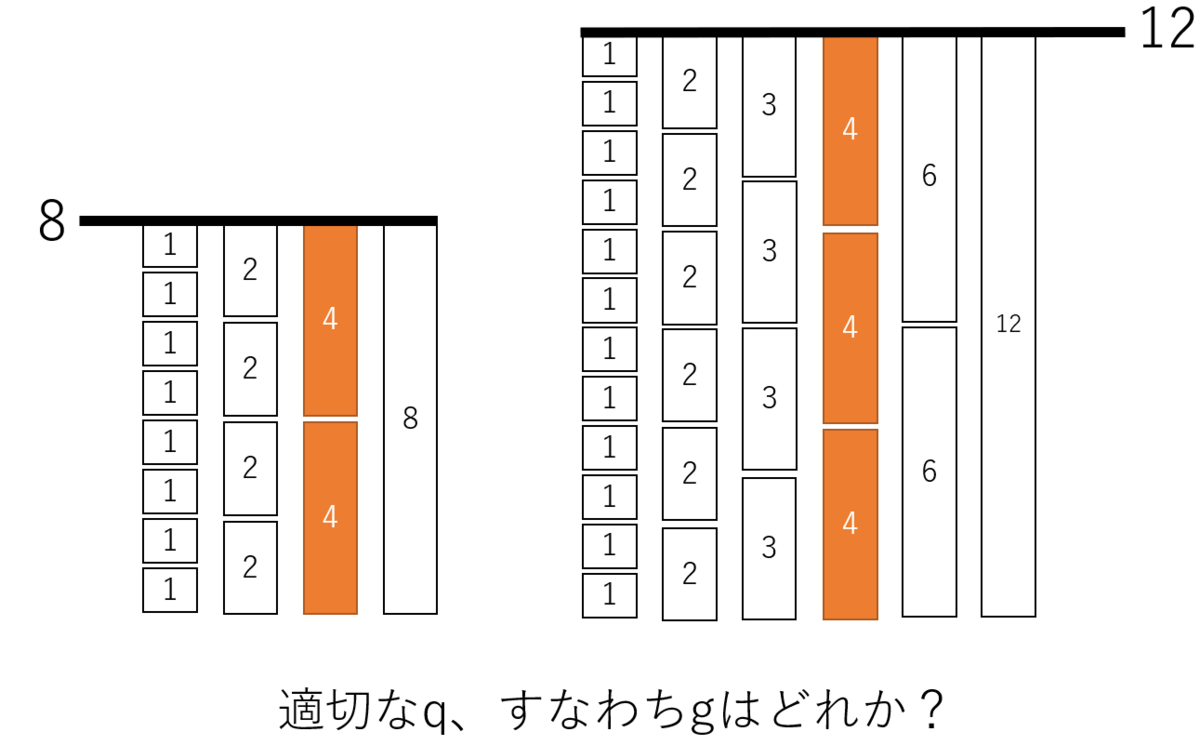
ユークリッドの互除法

ユークリッドの互除法の数式自体はいたってシンプルだ。以下の数式を元の正整数$a$と$b$に連鎖的に適応し続ければ、最大公約数が求められる。

$$ gcd(a, b) = gcd(b, a\bmod b) $$

この法則を拡張すると次のように、連鎖的に元の整数aとbを縮小することができる。
「$a_1$と$b_1$の最大公約数」$=$ 「$a_2=b_1$と$b_2=a_1\bmod b_1$の最大公約数」$=$「$b_2とa_2\bmod b_2$の最大公約数」=.....

例えば、a=30とb=16はユークリッドの互除法で以下のように連鎖的に縮小することができる。

「$a=30$ と$b=16$ の最大公約数」 $=$ 「$a_2=16$ と $b_2=30\bmod 16=14$の最大公約数」$=$ 「$a_3=14$と$b_3=16\bmod 14=2$の最大公約数」$=$「$a_4=2$と$b_3=14\bmod 2=0$の最大公約数」$= 2$

ちなみに、modはほとんど引き算と同じだ。言い換えると、a-bの拡張版がa%bだ。

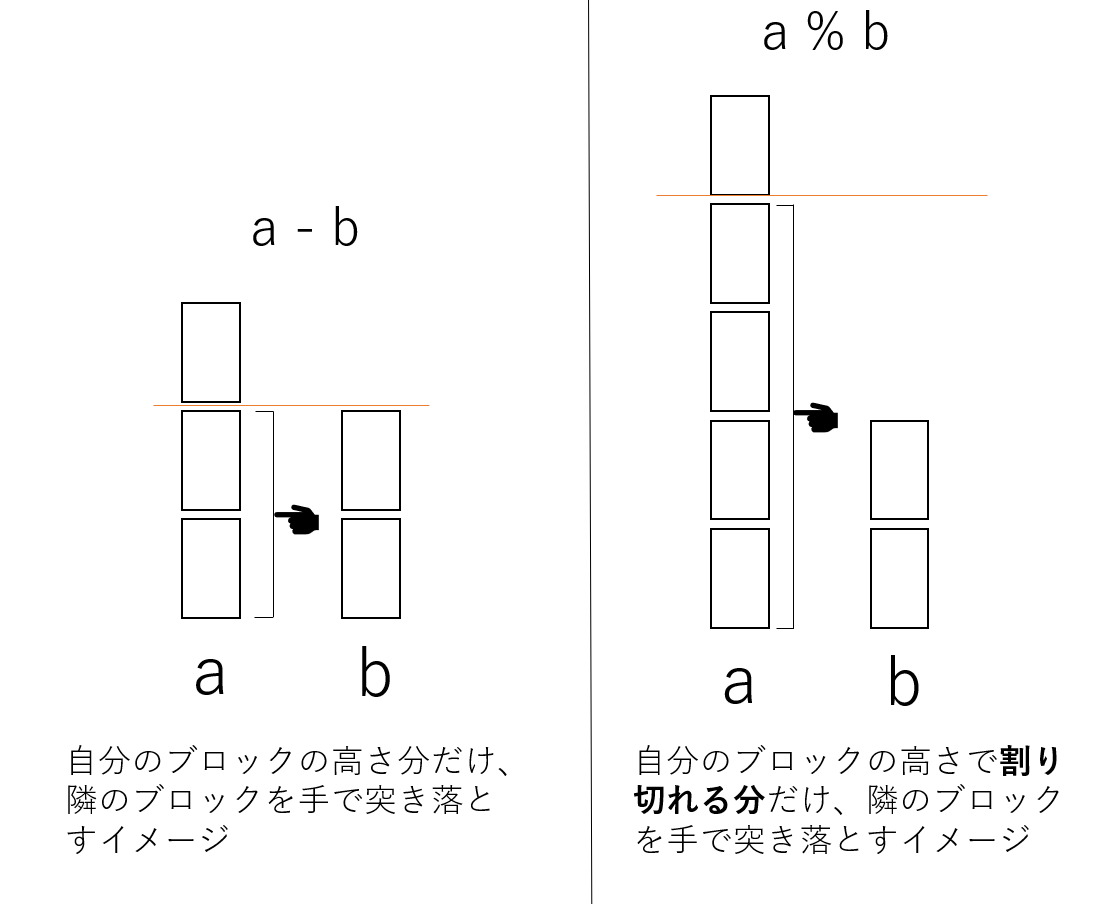
上では「-b」を繰り返しただろう。ただこの作業は以下のように省略することができる。

$$ a-b-b-b-b-b... =a-b*q = a\bmod q $$

• modは割った時のあまりを出す。（反対に割った時のquotientだけ出すのがfloor division //）
• NOTE: modはquotientを無視する。実際今回の場合quotientは必要ではない。

このように数式自体はシンプルなのだが、だからこそ、なぜそれが成り立つのが分かりにくい。以下のセクションではなぜユークリッドの互除法が成り立つのかを説明する。

なぜユークリッドの互除法は成り立つのか①

では、なぜこのアルゴリズムは最大公約数を求めることができるのだろうか。この問いを考える際に自ずと出てくる疑問は以下の二点だろう：

1. そもそもa%bは公約数g(=aとbの最大公約数)を持つのか？
2. a%bも公約数gを持っていたとして、これはbとa%bの「最大」公約数なのか？
3. なぜ最終的に元のgcdに帰結するのか？

そもそもa%bは公約数gを持つのか？

上でも述べたように、$a\bmod b$は$a-kb$と同義だ（$k$は$a/b$の商で、整数）。

よって、$a\bmod b$は以下のように表すことができる。

$$ a\bmod b = a - b×k = g×m - g×n×k=g(m - nk) $$

gで掛けられている形で表すことができるから、「$a\bmod b$」も$g$の倍数であるコトが分かる。

これをイメージとして理解するために$a\bmod b$を計算するプロセスを以下のように可視化してみる。

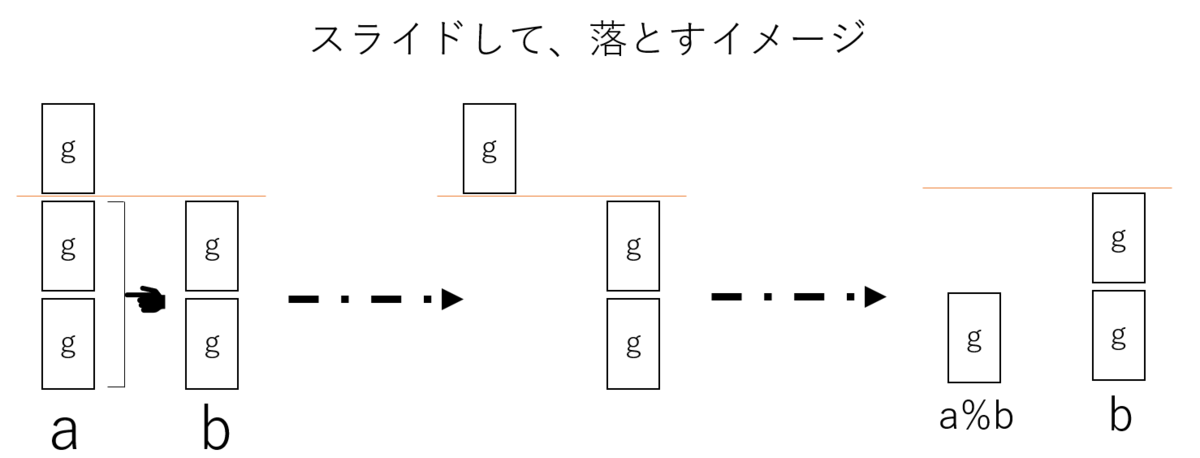
正整数aとbはどちらも同じサイズのブロック(同じ最大公約数g)で成り立つ。$a\bmod b$をするにあたって、$b$のブロック分だけ、$a$からブロックを「差し引き」している。ここがポイントで、もしブロックを削っていた場合は、$a-bk$は$g$の倍数ではなくなる。ブロックを「削る」のではなく、「差し引き」しているだけだからこそ、$a\bmod b$は必ず$g$の倍数になるのだ。

例えば、a=6とb=2の場合はこのように表すことができる

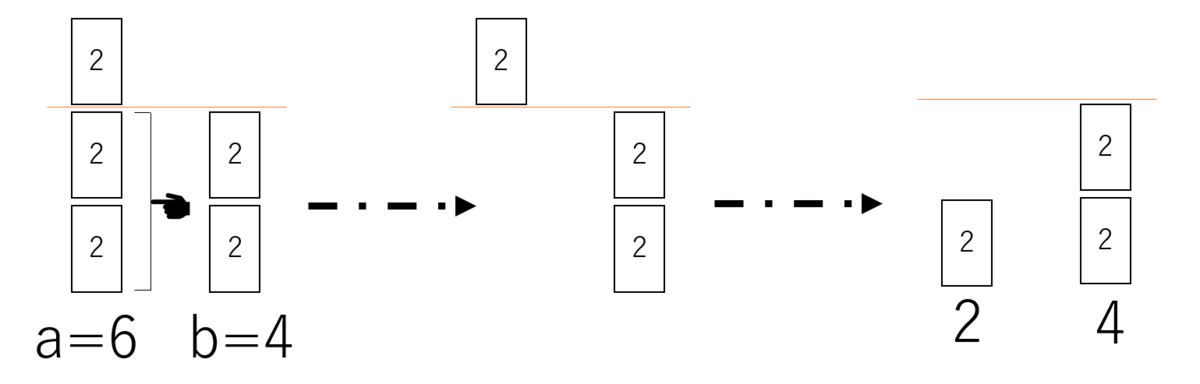
約数gを持っていたとして、これは「最大」公約数なのか？

a mod bが約数gを持っていたとき、自然と出てくる疑問が「このg(=aとbの最大公約数)はbとa mod bの最大公約数なのか」だ。

この問いを背理法で考える。gがbとa mod bの最大公約数でなかったとする。これはbとa mod bの間にgより大きい公約数g'が存在するということだ。 すでにbとa mod bに公約数gが必ず存在することは証明した。よって、bとa mod bは両方とも約数gを持つため、次のように表現できる。

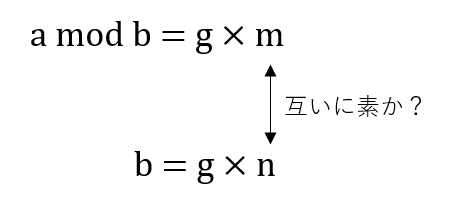
この時、もしgがbとa mod bの最大公約数であれば、mとnは必然的に互いに素である。反対に、最大公約数でなければ、互いに素ではなく、mとnには公約数があることが分かる。つまり、元の問は「mとnは互いに素か」という問いと同義で、この命題の真偽を証明すればよい。

証明に移る前に、これを視覚化する。mは「aについて、gのブロック数」、nは「bについての、gのブロック数」を表す。この時、mとnが互いに素ではない状況とは、aとbについてブロックの数に公約数があるということ。つまり、gが最大化できていない状況を意味する。

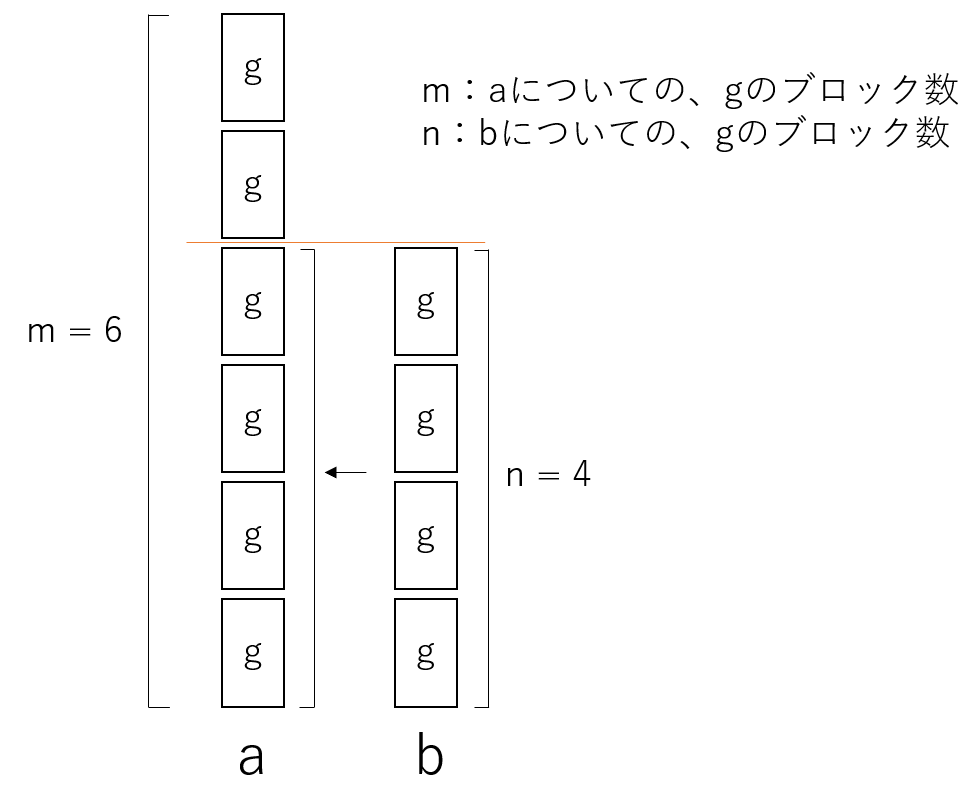
ここからは、命題「mとnは互いに素である」を証明する。つまり、mと(m mod n)は互いに素なのか？これを背理法で証明していく。

命題p = c1とc2が互いに素である場合、nと(m-nk)は互いに素
証明: pが偽であると仮定する(c2と(c1-c2)は互いに素ではない≡1より大きい公約数g’が存在する)。
\begin{align} \begin{cases} m-nk=p×c_1 & (1) \cr n=g×c_2 & (2) \end{cases} \end{align}
(1)を(2)に代入して、 $$ m - pc_2k = pc_1 $$ $$ ∴ m = pc_1+pc_2k $$ $$ ∴ m = p(c_1+c_2k) $$
c1とc2は互いで素であるはずが（前提）、両方ともpという（1より大きい）公約数が存在している。よって矛盾が生じている。
よって、仮定が間違っているから、 命題pは真。

なぜ最終的に元のgcdに帰結するのか？

今まで、「aとbの最大公約数がbとa mod bの最大公約数にも引き継がれる」ということを考えたてきた。元のaとbを各縮小ステップにおいて、この法則が成り立つ分かっただろう。しかし、これを繰り返した果てに、元のgcdに帰結するというのが、感覚的に分かりにくい。故に、このセクションでは「縮小を連続すると、最大公約数にたどり着く」ことを説明する。

また、整数をブロックでイメージすると、互換法は以下のように解釈できる。

1. 片方ずつ隣のブロックをスライドして落とし続ける
2. いつか片方のブロックがなくなる
3. そのとき残るのは一つのブロックg（＝最大公約数）だけ

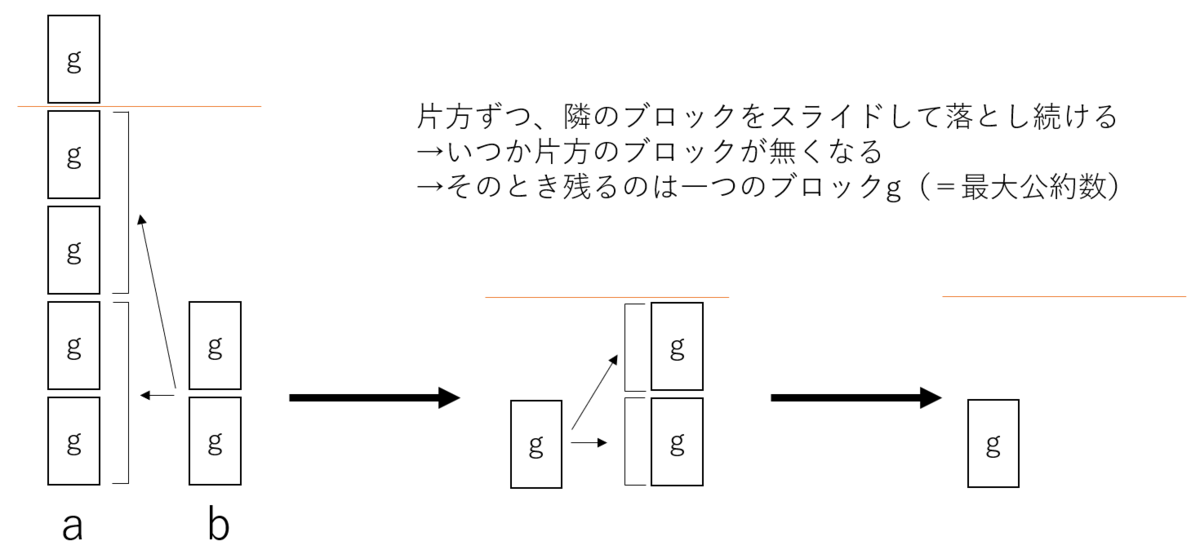
三つ目のポイント「残るのが一つのブロック」の理由は、そうでないと矛盾が生じるからだ。つまり、次のようなaとbが存在していたとする。 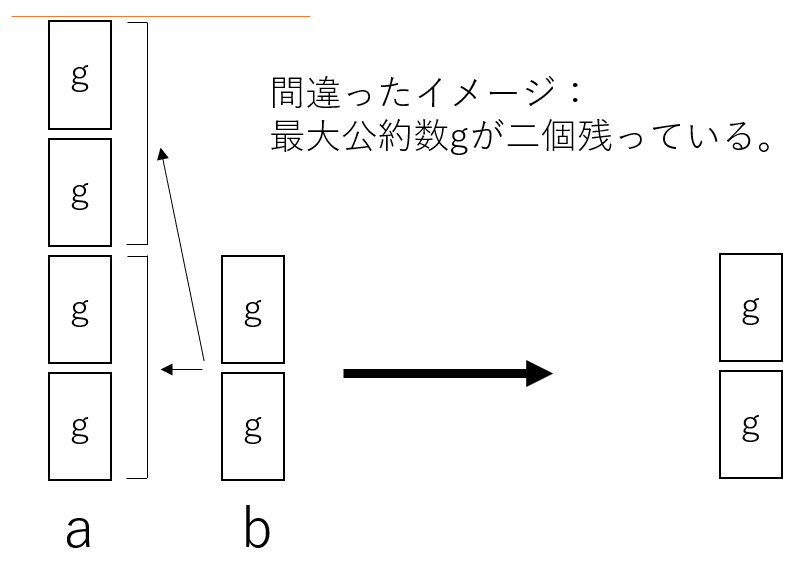最後に二つのブロックが残っているため、一見、必ずしも最後に残るブロックは一つではないように見える。しかし、実際にはこの状況はあり得ない。なぜならば、そもそものaとbの「gの個数」に公約数が存在してしまっているから。 \begin{align} \begin{cases} a = g×4\cr b=g×2 \end{cases} \end{align} ある整数aとbについての最大公約数gを定義する際には、それぞれgにすべての公約数が「集約」されている必要がある。つまり、m (今回の場合は4)とn (今回の場合は2)は互いに素であるべきであるのに反して、2という公約数が存在してしまっているのだ。故に、矛盾が生じていて、この例は「残るのが一つのブロック」への反例にはなりえない。

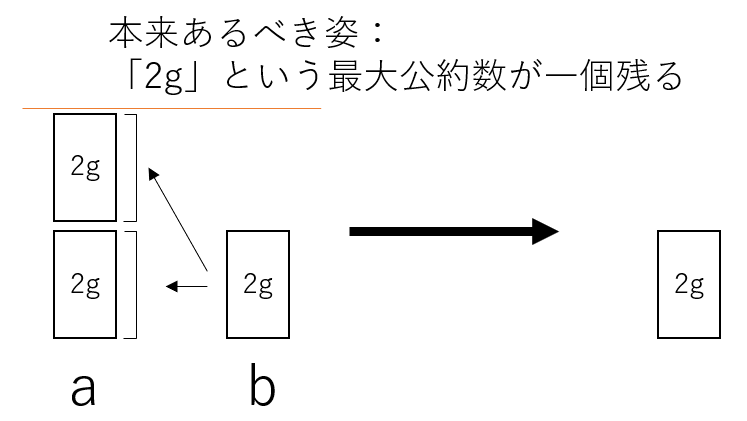
本来、この例の最大公約数は2gであるべきだ。

\begin{align} \begin{cases} a = (2g)×2\cr b=(2g)×1 \end{cases} \end{align}

こうすることで、mとnはそれぞれ、2と1で、公約数は存在しなく、互いに素なことが分かる。

なぜユークリッドの互除法は成り立つのか②

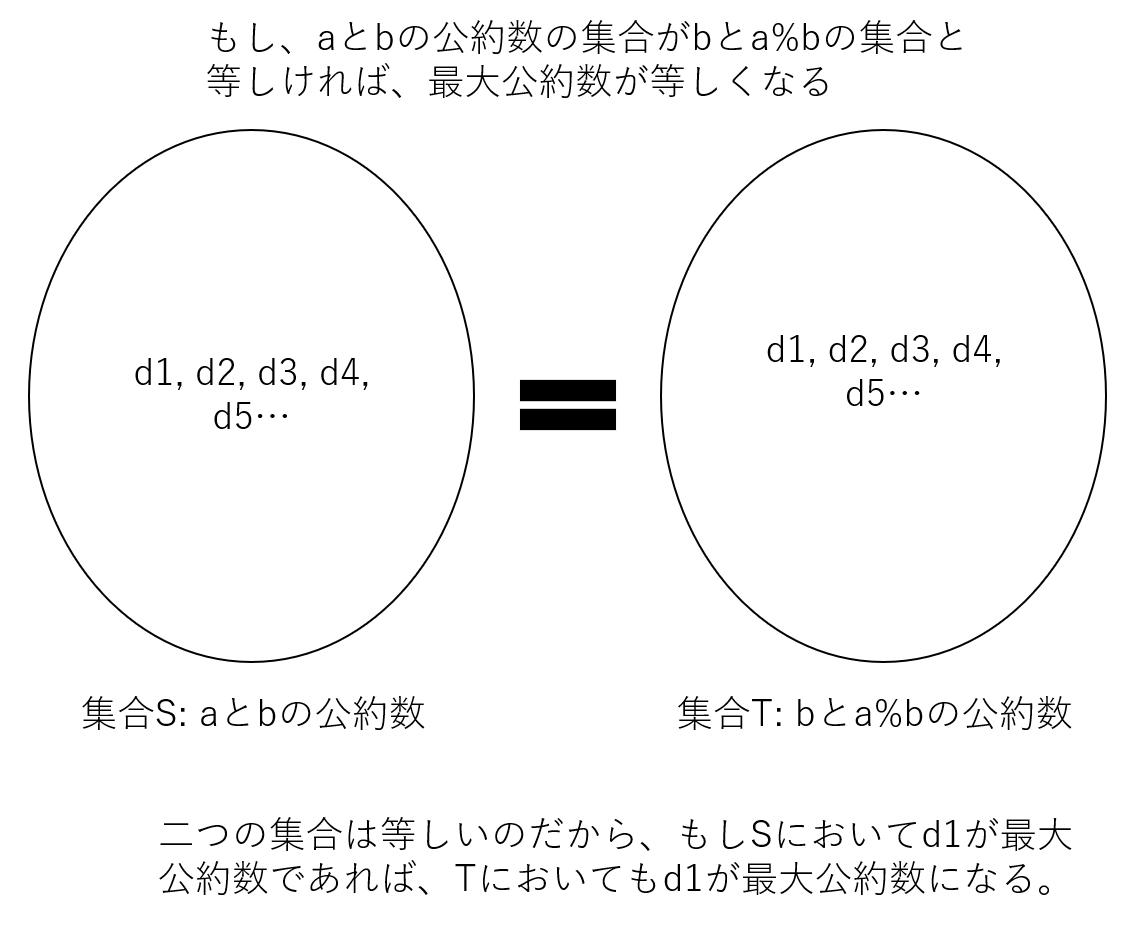
ユークリッドの互除法の理解方法をもう一つ紹介する。これはaとbの公約数の集合を考える方法だ。

1. もし、aとbの公約数が、bとa mod bの公約数と同じであれば、
2. 必然的に、aとbの最大公約数は、bとa mod bの最大公約数と等しくなる

二つ目の論理は自明だが、一応図示しておく。

では最初のポイントを命題として、証明してみる。

$$ S = \{d: d = cd(a, b)\} $$ $$ T = \{e: e = cd(b, a\bmod b)\} $$ （cdは公約数を指す）としたとき、証明したい命題は、「集合SとTは等しい」だ。この命題を証明するには、次の二つの「サブ命題」を証明する必要がある。
1. dがSに属する→dがTに属する [aとbの公約数→bとa%bの公約数]
2. eがTに属する→eがSに属する[bとa%bの公約数→aとbの公約数]

「dがSに属する→dがTに属する」の証明：

ある整数dを正整数aとbの公約数とする。 \begin{align} \begin{cases} a=dm & (1) \cr b=dn & (2) \end{cases} \end{align} mとnはそれぞれ整数。(1)を(2)を$a\bmod b$ に代入する。 $$ a mod b = a - bk = dm - dnk = d(m - bk) (3) $$
(2)と(3)より、Sに属するdは、Tにも属する。すなわち、あるaとbの公約数dは、bとa mod bの公約数でもある。□

「eがTに属する→eがSに属する」の証明

\begin{align} \begin{cases} a-bk = em & (1) \cr b = en & (2) \end{cases} \end{align}
(1)を展開する $$ a = em + bk $$ (2)を代入して、 \begin{split} a& = em + enk\cr & = e(m + nk) & (3) \end{split}
(2)と(3)より、Tに属するeは、Tにも属する。すなわち、あるbとa mod bの公約数eは、aとbの公約数でもある。□

よって、「dがSに属する→dがTに属する」と「eがTに属する→eがSに属する」を証明したため、「集合SとTは等しい」、すなわち、「aとbの公約数が、bとa mod bの公約数が同じである」ことを証明したことになる。
したがって、必然的に、aとbの最大公約数は、bとa mod bの最大公約数と等しくなる。つまり、ユークリッドの互除法を証明したということになる。

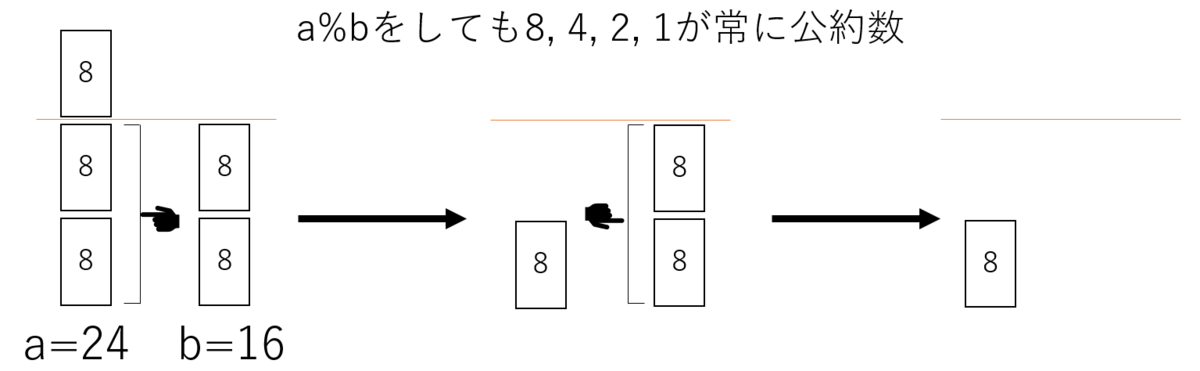
これは直観的にも理解しやすい。以下のように、a%bを繰り返しても、aとbの公約数は常に最大公約数と、最大公約数自体の約数だ。

独立な試行

私が確立の分野で特に挫折したのが「独立」という概念だ。まず独立とは、P(A) = P(A|B)が成り立つある事象AとBの関係のことだと学ぶ。さらにP(A|B)=P(A∩B)/P(B)を利用して、P(A)P(B) = P(A∩B)でも独立であることを証明できると教えられる。しかし、これらはどこか直観的に理解しにくく、また視覚的にもイメージしにくい部分が残る（一方で排反事象はベン図で見れば簡単に理解できる）。そこで今回は、「独立」を視覚的に現せるか考えてみた。

明らかに独立・独立でないケース

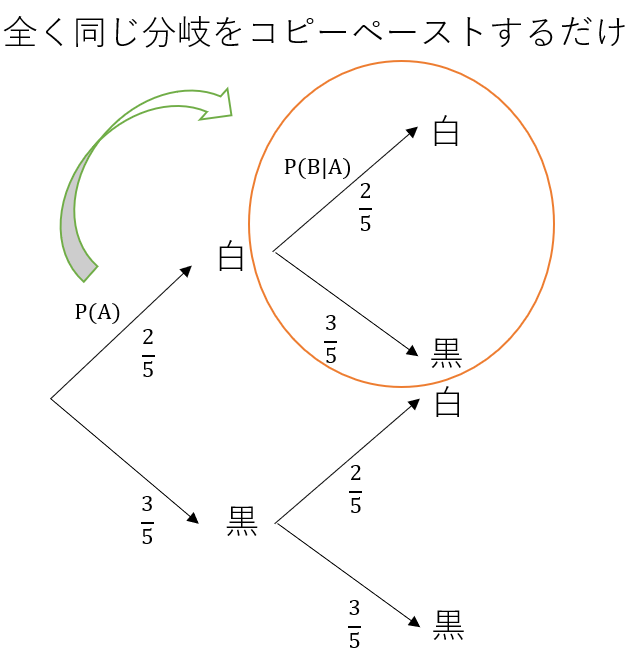
明らかに独立である試行の例として反復試行が挙げられる。例えば白玉が二つ、黒玉が三つ入った箱から一つ玉を引いて、戻してもう一度引くという操作を繰り返すとする。事象Aを「一回目の引きで白が出る」、事象Bを「二回目の引きで白がでる」と定義し、公式通りに計算するとこれらが独立なことが分かる。

P(B) = 2/5

P(B|A) = 2/5

よってP(B|A) = P(B)が成り立ち、AとBが独立であることが分かる。

これは直観的にも明らかで、同じ試行を繰り返すだけということは樹形図にそのまま同じ文意をコピーペーストすればよいだけだ。つまりP(B|A)がP(A)と違くなるわけがない。

一方で、一度引いたらもとに戻さないで上と同様の試行を繰り返すと：

P(B) = 2/5

P(B|A) =  1/4

P(B)とP(B|A)は等しく無いため、AとBは独立でないことが分かる。

これも直観的に明らかで、すでに白が引かれた状態であれば（元に戻さないため）、箱の中に白が入っている確率は明らかに変化する。

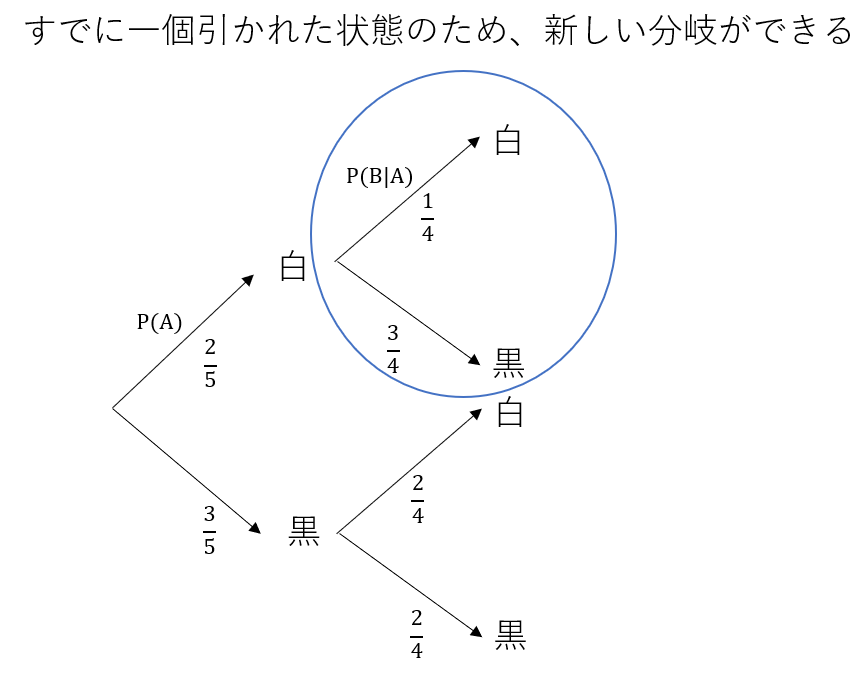
トランプで考えてみる

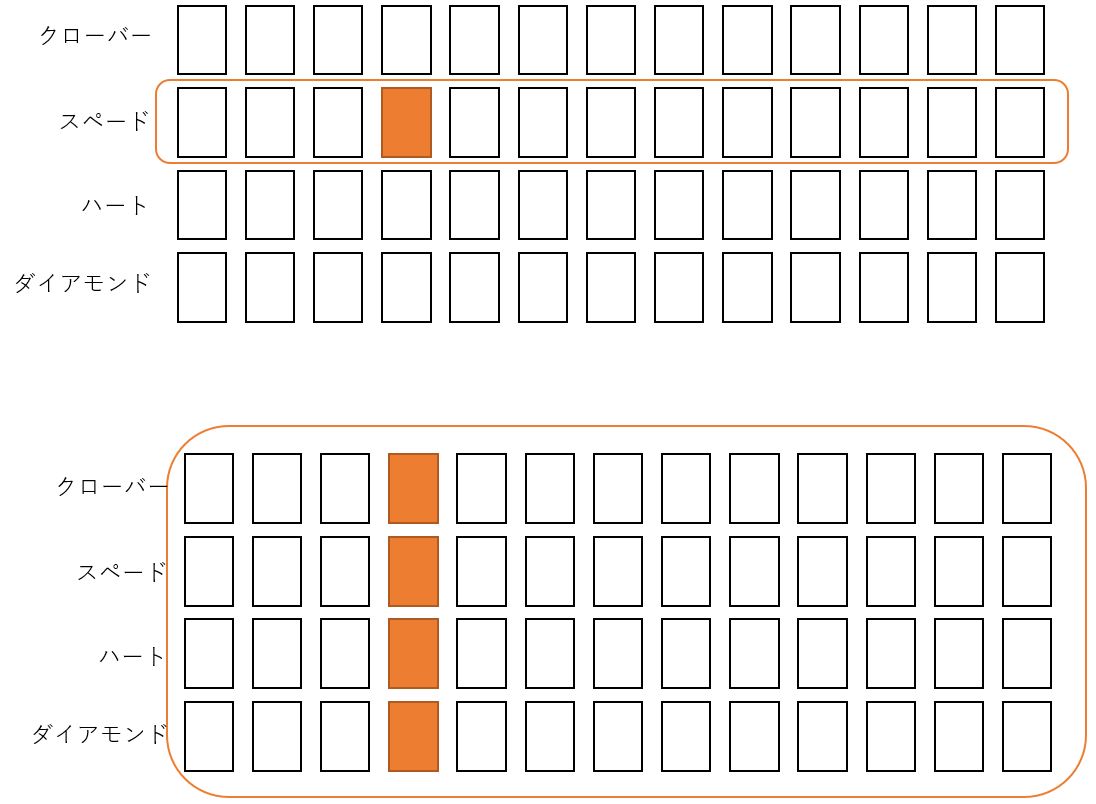
トランプセットから一枚ランダムに抜き取り、事象Aと事象Bがそれぞれ次のように定義されていたとする。

事象A: 4のカードが出る

事象B: スペードのカードが出る

これらが独立かどうかを検証しよう。つまり、「全体からトランプカードを引くとき4が出る確率」 vs. 「ハートを引いたとしてそのカードが4である確率」について考える。

上図を見ていただければわかるように、

P(A) = 4のカードの枚数/全部のカードの枚数＝ 4/52 = 1/13

P(A|B) = スペードで4のカードの枚数/スペードの枚数 = 1/13

P(A) = P(A|B) = 1/13だから、この二つの事象は独立しているといえる。

結論

以上、二つのセクションを通して独立について再考した。まず「交換あり」と「交換なし」の試行について独立性を調べた。そして、トランプの例で独立のイメージがさらに強くなったと思う。基本的に、独立を強くイメージする上で以下が重要なポイントだろう：

1. 樹形図や問題に適応させた図（例えばトランプカードが並べられた図）などをまず描く

2. 全体: P(A) と  P(A) : P(A∩B)を比較する。これはBが起きる以前のAの確率と、Bが起きた後の（樹形図で言う、Bという分岐を選んだ時に）Aの確率に変化があるかがを調べているということ。

3. 確率というのは一種の「比率」であって、P(A)が絶対的な比率なことに対して、P(A|B)はBをベースにした相対的な比率。この比率に変化があるかどうかが独立性の決め手となる。

4. トランプカードの例を「独立性」の象徴的な例と捉えると分かりやすいと思う。特に「全体からトランプカードを引くとき4が出る確率」 vs. 「ハートを引いたとしてそのカードが4である確率」についてどちらも1/13だからこそ、この二つの事象は独立しているということを理解する。（逆に反復試行の例は少し特殊な例のため、この問題での独立をすべての問題に適応するのは難しいだろう。）

掛け算と場合の数

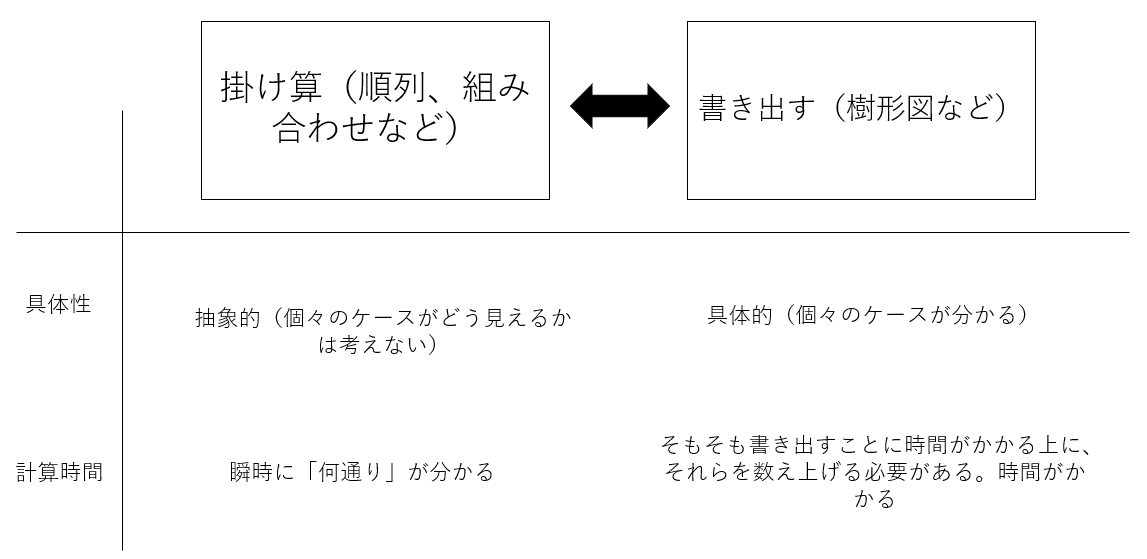
私が場合の数を初めて学んだのは中学生の時だったが、当時挫折したことを覚えている。その原因は掛け算の本質を理解できていなかったから。実は、積は計算プロセスを省略可してくれるという意味で、和・差と比較するととてもパワフルな計算手法だ。その分、積は抽象的な考え方となるため、イメージが大事となる（だからこそ当時の私は挫折したのだろう）。今回はそんな掛け算の根本的な意味を再考すると同時に、それが場合の数を計算する上で同応用できるのかを検証する。

掛け算の根本的な考え方

小学校で学ぶ掛け算の代表的な例を挙げてみる。「鉛筆が3ダースある。合計でいくつあるか。」この答えは勿論12×3=36なのだが、重要なのは計算手順よりも、この計算の意味だ。この際イメージすべきなのは：

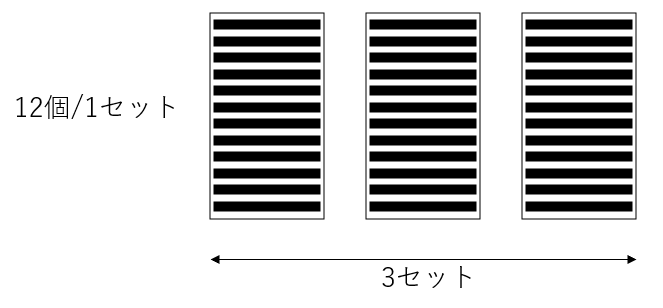
これを数式に表すと、12個/1ダース × 3個分 = 36個となる。つまり掛け算とは一般的に一つのセットにつき何個あるか×それが何セット分あるかというものなのだ。

小学生はこれらをそれぞれ掛けられる数と掛ける数と教わり、それらの順番を間違えただけでバツにされることもあるが、順番はどうでもよい。大事なのは、それらの意味としての区別を確実につけることだ。つまり、「12個/1セットが3個ある」と考えようが、「3個の12個/1セットがある」と考えるかはどちらでもよいのだが、12は〇個/1セットの部分であって、3はそれが何個あるかの部分であるという認識を持つ必要があるのだ。

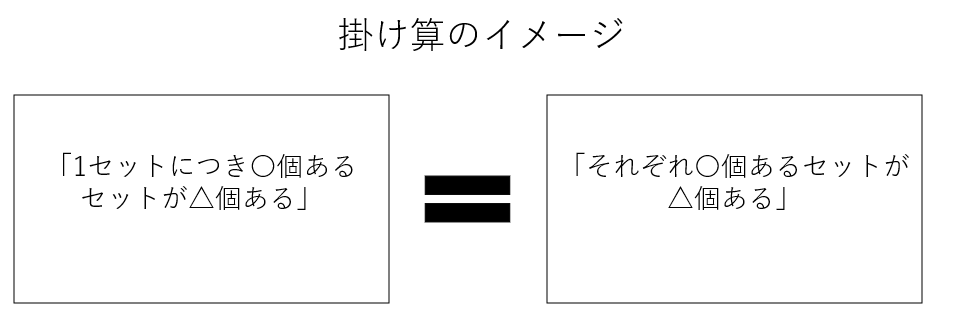
本質：掛け算のイメージは「1セットにつき〇個あるセットが〇個ある」だ。「1セットにつき」を「それぞれ」や「おのおの」に置き換えることもできる。これらが掛け算のキーワードだ。

掛け算と場合の数の関わり

学んだことがある人ならば誰でもわかると思うが、場合の数は掛け算で溢れている。それは掛け算を用いることで「何通り」をショートカットして考えることができるからだ（冒頭で述べたように掛け算はパワフルなツールなのだ）。

「ある事象が何通り起こりうるか？」を愚直に解こうとする場合、すべてのケースを書き出しそれらを数え上げるだろう。例えば、樹形図を描いたり、辞書のように順序だててすべてのケースを書きだすこともできる。一方で掛け算を使えば具体的なケースに触れずとも（これは問題によってはデメリットにもなりうるが）、「何通り」かが瞬時にわかる。

例えば、「0~9の数字を使って8桁の数字は何通り作れるか」という問題について、愚直に樹形図を描いて数字の個数を数えていては時間の無駄だが「順列」という名の掛け算を使えば10秒もせずに答えを導き出せるのだ。

しかし、なぜ掛け算を用いて場合の数を計算できるのだろうか。これを理解するのにこそ掛け算の根本的な意味が大事なのだ。ここからは場合の数と掛け算のつながりを具体的に示す。

サイコローコインで考える

まずは分かりやすい例から始める。「サイコロを振った後に、コイントスをしたとき、何通りの（サイコロの目, コインの裏表）のペアが考えられるか」という問題に対して樹形図を描くと以下のようになる。

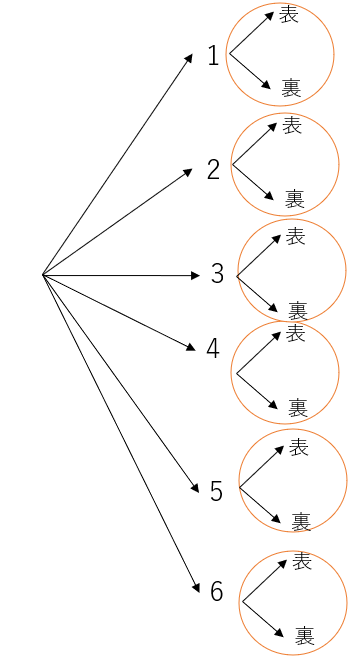
(表, 裏)が六つあるがこれはコインを6回降るわけではない（当たり前だが）。すべてのペアを考慮する上で「それぞれ2通り（表と裏）ある事象が、サイコロの結果（1, 2, 3, 4, 5, 6）の個数分だけ必要なのだ」。この表現がすでに述べた積の表現と対応することを理解して欲しい。新たな事象の結果が二通りあれば、それをこれまでのすべての道筋分だけ用意する必要があるのだ。だからこそ、2×6=12通りの結果が考えられるのだ。

式の項数で考える

もう少し抽象的な例を見てみる。「(a+b+c)(e+d)を展開した際の項数は何個あるか」という問題があったとする。これについて樹形図を描いてみる。

この樹形図を先ほど述べた掛け算の意味合い的に見ると「それぞれ2通りある（d, e）選択肢が3個分（a, b, c）だけ必要」なのだ。「2個/1セットが3個分ある」と持言い換えられる。aについて(d,e)が、bについても(d,e)が、そしてcについても(d,e)の選択肢がある。これは逆に「3個分の2個/1セットがある」とも捉えれれる。故に答えは、3×2＝6となるのだ。

では、(a+b+c)(e+d)(f+g+h+i)を展開したときの項数は何個あるだろうか。このような三次元以上の問題を分かりやすく理解したければ、分解化することを考えればよい。(a+b+c)(e+d)(f+g+h+i)は [(a+b+c)(e+d)]×(f+g+h+i)と二つの部分に分解できる。 [(a+b+c)(e+d)]の部分は先ほど計算した通り6通りある（ad, ae, bd, be ,cd, ce）。故に下図のような樹形図ができる。

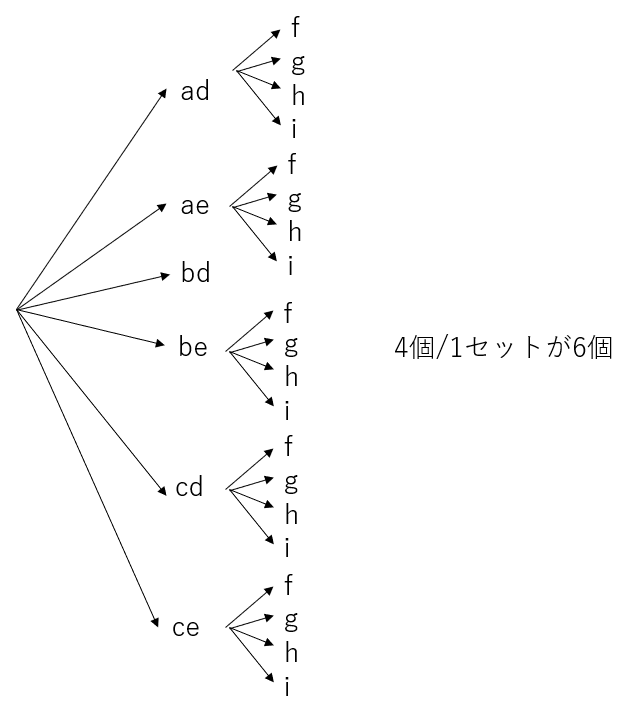
この場合、4個/1セットが6個ある（6個が、それぞれ4個ずつ分岐する）ことが分かるだろう。だから6×4=24なのだ。

慣れてくれば、わざわざ分解化する必要もなくなる。当たり前ではあるが掛け算は総合的（associative）なため、(a+b+c)(e+d)(f+g+h+i) = [(a+b+c)(e+d)](f+g+h+i)が成り立つ。故に上図のような(2×3)×4と2×3×4は同じことだ。

結論

場合の数に挫折する同級生をよく見かけるが、（私と同じであれば）その原因が掛け算の本質を理解しきれていない部分にあることも考えられる。

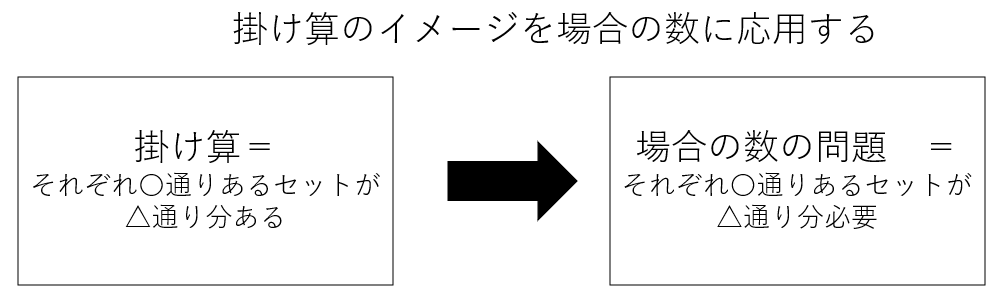
掛け算の根本的な意味（すなわち、それぞれ〇通りあるセットが△通り分ある）、場合の数の問題の意味（それぞれ〇通りあるセットが△通り分必要）、そしてだからこそなぜ掛け算が場合の数を計算する上で応用することができるのか。これらを理解することで抽象的な場合の数の計算方法のイメージを鮮明にすることができると信じている。