掛け算と場合の数

私が場合の数を初めて学んだのは中学生の時だったが、当時挫折したことを覚えている。その原因は掛け算の本質を理解できていなかったから。実は、積は計算プロセスを省略可してくれるという意味で、和・差と比較するととてもパワフルな計算手法だ。その分、積は抽象的な考え方となるため、イメージが大事となる（だからこそ当時の私は挫折したのだろう）。今回はそんな掛け算の根本的な意味を再考すると同時に、それが場合の数を計算する上で同応用できるのかを検証する。

掛け算の根本的な考え方

小学校で学ぶ掛け算の代表的な例を挙げてみる。「鉛筆が3ダースある。合計でいくつあるか。」この答えは勿論12×3=36なのだが、重要なのは計算手順よりも、この計算の意味だ。この際イメージすべきなのは：

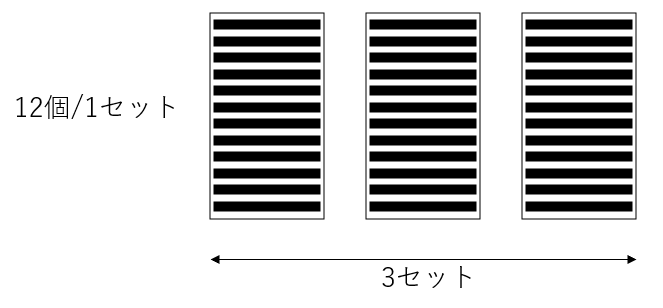
これを数式に表すと、12個/1ダース × 3個分 = 36個となる。つまり掛け算とは一般的に一つのセットにつき何個あるか×それが何セット分あるかというものなのだ。

小学生はこれらをそれぞれ掛けられる数と掛ける数と教わり、それらの順番を間違えただけでバツにされることもあるが、順番はどうでもよい。大事なのは、それらの意味としての区別を確実につけることだ。つまり、「12個/1セットが3個ある」と考えようが、「3個の12個/1セットがある」と考えるかはどちらでもよいのだが、12は〇個/1セットの部分であって、3はそれが何個あるかの部分であるという認識を持つ必要があるのだ。

本質：掛け算のイメージは「1セットにつき〇個あるセットが〇個ある」だ。「1セットにつき」を「それぞれ」や「おのおの」に置き換えることもできる。これらが掛け算のキーワードだ。

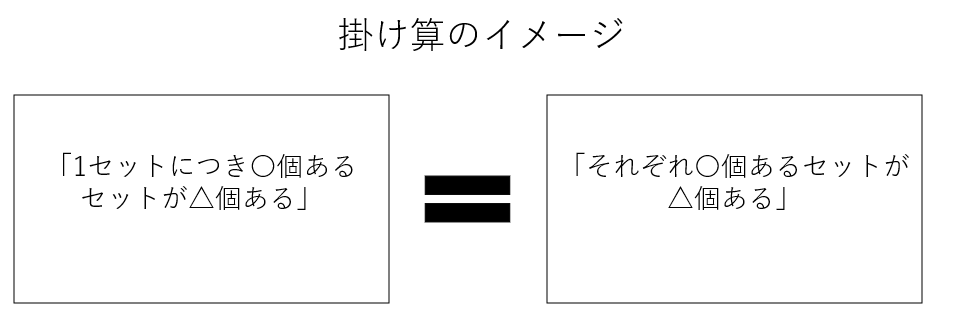
掛け算と場合の数の関わり

学んだことがある人ならば誰でもわかると思うが、場合の数は掛け算で溢れている。それは掛け算を用いることで「何通り」をショートカットして考えることができるからだ（冒頭で述べたように掛け算はパワフルなツールなのだ）。

「ある事象が何通り起こりうるか？」を愚直に解こうとする場合、すべてのケースを書き出しそれらを数え上げるだろう。例えば、樹形図を描いたり、辞書のように順序だててすべてのケースを書きだすこともできる。一方で掛け算を使えば具体的なケースに触れずとも（これは問題によってはデメリットにもなりうるが）、「何通り」かが瞬時にわかる。

例えば、「0~9の数字を使って8桁の数字は何通り作れるか」という問題について、愚直に樹形図を描いて数字の個数を数えていては時間の無駄だが「順列」という名の掛け算を使えば10秒もせずに答えを導き出せるのだ。

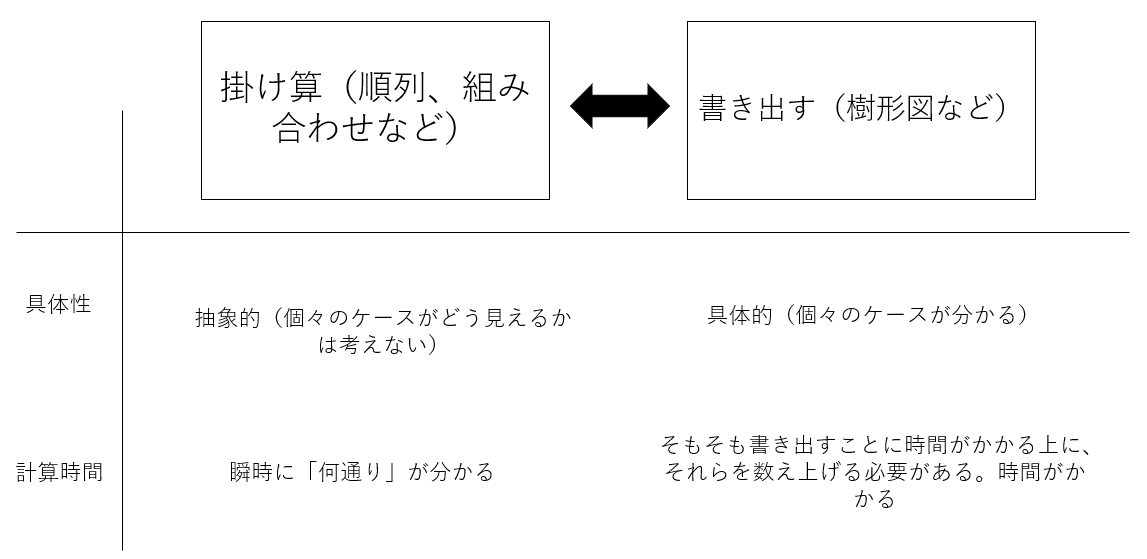
しかし、なぜ掛け算を用いて場合の数を計算できるのだろうか。これを理解するのにこそ掛け算の根本的な意味が大事なのだ。ここからは場合の数と掛け算のつながりを具体的に示す。

サイコローコインで考える

まずは分かりやすい例から始める。「サイコロを振った後に、コイントスをしたとき、何通りの（サイコロの目, コインの裏表）のペアが考えられるか」という問題に対して樹形図を描くと以下のようになる。

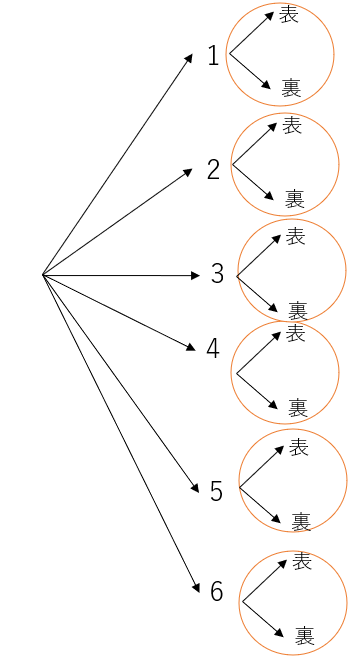
(表, 裏)が六つあるがこれはコインを6回降るわけではない（当たり前だが）。すべてのペアを考慮する上で「それぞれ2通り（表と裏）ある事象が、サイコロの結果（1, 2, 3, 4, 5, 6）の個数分だけ必要なのだ」。この表現がすでに述べた積の表現と対応することを理解して欲しい。新たな事象の結果が二通りあれば、それをこれまでのすべての道筋分だけ用意する必要があるのだ。だからこそ、2×6=12通りの結果が考えられるのだ。

式の項数で考える

もう少し抽象的な例を見てみる。「(a+b+c)(e+d)を展開した際の項数は何個あるか」という問題があったとする。これについて樹形図を描いてみる。

この樹形図を先ほど述べた掛け算の意味合い的に見ると「それぞれ2通りある（d, e）選択肢が3個分（a, b, c）だけ必要」なのだ。「2個/1セットが3個分ある」と持言い換えられる。aについて(d,e)が、bについても(d,e)が、そしてcについても(d,e)の選択肢がある。これは逆に「3個分の2個/1セットがある」とも捉えれれる。故に答えは、3×2＝6となるのだ。

では、(a+b+c)(e+d)(f+g+h+i)を展開したときの項数は何個あるだろうか。このような三次元以上の問題を分かりやすく理解したければ、分解化することを考えればよい。(a+b+c)(e+d)(f+g+h+i)は [(a+b+c)(e+d)]×(f+g+h+i)と二つの部分に分解できる。 [(a+b+c)(e+d)]の部分は先ほど計算した通り6通りある（ad, ae, bd, be ,cd, ce）。故に下図のような樹形図ができる。

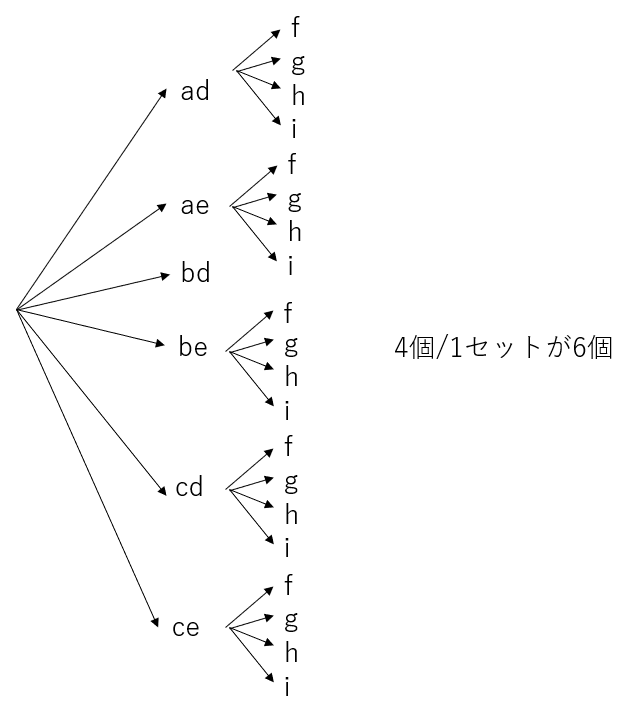
この場合、4個/1セットが6個ある（6個が、それぞれ4個ずつ分岐する）ことが分かるだろう。だから6×4=24なのだ。

慣れてくれば、わざわざ分解化する必要もなくなる。当たり前ではあるが掛け算は総合的（associative）なため、(a+b+c)(e+d)(f+g+h+i) = [(a+b+c)(e+d)](f+g+h+i)が成り立つ。故に上図のような(2×3)×4と2×3×4は同じことだ。

結論

場合の数に挫折する同級生をよく見かけるが、（私と同じであれば）その原因が掛け算の本質を理解しきれていない部分にあることも考えられる。

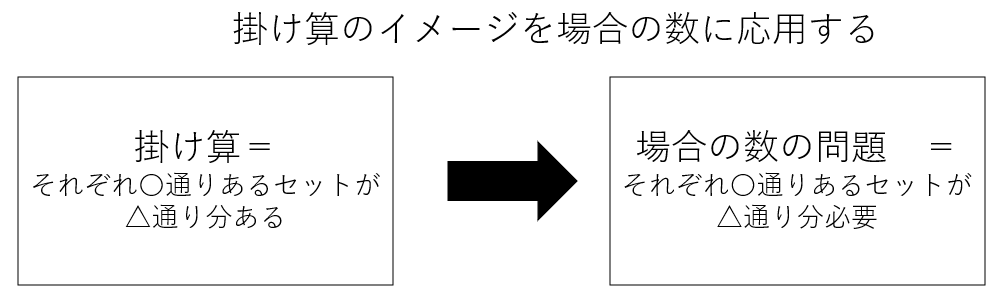
掛け算の根本的な意味（すなわち、それぞれ〇通りあるセットが△通り分ある）、場合の数の問題の意味（それぞれ〇通りあるセットが△通り分必要）、そしてだからこそなぜ掛け算が場合の数を計算する上で応用することができるのか。これらを理解することで抽象的な場合の数の計算方法のイメージを鮮明にすることができると信じている。